Pass the Hash (Warmup/Learning; 50 points)

Solved by Mystiz.

Challenge Summary

We are given a peculiar hash algorithm that generates 64-byte long hashes, which wraps of sha0, sha1, sha256 and ripemd160. The hash takes two arguments, salt (20 bytes) and password (22 bytes). We are allowed to control the salt, whilst the goal is to find the password within 1024 queries.

Hash construction

We are given a peculiar hash algorithm that generates 64-byte long hashes, which wraps of sha0, sha1, sha256 and ripemd160.

The hash is defined by:

  1. $L_0, R_0 = \text{password}\ |\ \text{salt}\ |\ \text{password}$ ($L_0, R_0$ separate the 64-byte block)
  2. $L_{i+1} = L_i \oplus h_R(R_i), R_{i+1} = R_i \oplus h_L(L_i)$, for $i = 0, 1, ..., 15$.

Here $h_L$ and $h_R$ are the two hash algorithms that uses one of the commonly used hash algorithms based on the content. As this is a 32-byte block, if the hash algorithm itself does not consist 32 bytes, it would repeat itself until there are 32 bytes.

Solution

Part I: Repeat, repeat, repeat

One question that had brought up to my mind is: What if the $h_L$ and $h_R$ uses solely the 20-byte hash algorithms (i.e., all but sha256)?

Assume that 20-byte hash algorithms are used. Let's see what will happen in a round.

Define $s_0\ |\ s_1\ |\ ...\ |\ s_9 := L_i\ | \ R_i$ and $t_0\ |\ t_1\ |\ ...\ |\ t_9 := L_{i+1}\ | \ R_{i+1}$, where:

  • $s_0, s_2, s_3, s_6, s_7, s_9, t_0, t_2, t_3, t_6, t_7, t_9$ are 8 bytes long, and
  • $s_1, s_4, s_5, s_8, t_1, t_4, t_5, t_8$ are 4 bytes long.

Then we have:

  1. $t_0\ |\ t_1\ |\ ...\ |\ t_4 = s_0\ |\ s_1\ |\ ...\ |\ s_4\ |\ h_R(s_5\ |\ s_6\ |\ ...\ |\ s_9)$, and
  2. $t_5\ |\ t_6\ |\ ...\ |\ t_9 = s_5\ |\ s_6\ |\ ...\ |\ s_9\ |\ h_L(s_0\ |\ s_1\ |\ ...\ |\ s_4)$.

However, since the first and last 12 bytes of $h_R(\cdot)$ are equal, we have

  1. $s_0 \oplus t_0 = s_3 \oplus t_3$, and
  2. $s_1 \oplus t_1 = s_4 \oplus t_4$.

The assumption applies on $h_L(\cdot)$ as well. Thus we have

  1. $s_5 \oplus t_5 = s_8 \oplus t_8$, and
  2. $s_6 \oplus t_6 = s_9 \oplus t_9$.

If we define $L_0, R_0$ by $a_0, a_1, …, a_9$ and $L_{16}, R_{16}$ by $b_0, b_1, …, b_9$ (their lengths are respectively equal to $s_0, s_1, …, s_9$), we still have the below properties:

  1. $b_0 \oplus b_3 = a_0 \oplus a_3$,
  2. $b_1 \oplus b_4 = a_1 \oplus a_4$,
  3. $b_5 \oplus b_8 = a_5 \oplus a_8$, and
  4. $b_6 \oplus b_9 = a_6 \oplus a_9$.

Part II: What does it mean?

Let's look back how $L_0, R_0$ is defined - $\text{password}\ |\ \text{salt}\ |\ \text{password}$. This gives us two more properties:

  1. $a_0 = a_7, a_1 = a_8, a_2 = a_9$ (derived from passwords), and
  2. we can control the values of $a_3, a_4, a_5, a_6$.

So... assuming that $h_L$ and $h_R$ uses solely the 20-byte hash algorithms, we can effectively find the password (namely $a_0, a_1, a_2$):

  1. $a_0 = a_3 \oplus b_0 \oplus b_3$,
  2. $a_1 = a_4 \oplus b_1 \oplus b_4$ and
  3. $a_2 = a_9 = a_6 \oplus b_6 \oplus b_9$.

Part III: But the assumption is too good to be true!

As stated from the title, the assumption is quite hard to satisfy. What we need is, in each of the 16 rounds, $h_L$ and $h_R$ needs to pick an 20-byte hash algorithm instead of the 32-byte hash algorithm... Very difficult isn't it?

The answer is not really. The probability to use 20-byte hash algorithms all along is $0.75^{32}\approx 0.000145257$, which is approximately one out of 10000. We can visit the oracle 10 times, in average, to compute the password from the hash algorithm.

It is very easy to know when we had the hash algorithm. From properties 2 and 3, we have:

\[b_1 \oplus b_4 \oplus b_5 \oplus b_8 = a_1 \oplus a_4 \oplus a_5 \oplus a_8 = a_4 \oplus a_5.\]

Writing the exploit script solving the challenge, we have the flag: PTBCTF{420199e572e685af8e1782fde58fd0e9}.

Avec? (Cryptanalysis; 856 points)

Solved by harrier.

Challenge Summary

This is a interesting question where we are given a ciphertext, encrypted using AES-GCM, with key and nonce generated by polish_key(os.urandom(8)) and concat itself. The key and nonce is not provided though, so we have to somehow reverse the polish_key process to know more about the key and nonce.

Solution

I first thought this is a GCM nonce collision problem, but the 12 bytes nonce and nonce generation rejects this thought.

The polish_key function is the following:

def polish_key(key):
	key = bytes_to_long(key[::-1])
	key = GF(2**64).fetch_int(key)
	key = key ** 0xbcafffff435
	key = long_to_bytes( key.integer_representation() )[::-1]
	assert len(key) == 8
	return key

Which 0xbcafffff435 is can be factored into $3\times5\times7\times257\times3019\times65537$. Knowing that $3^{32} - 1 = 3\times5\times7\times257\times65537$, the key is of order $3^{32}+1$ (or a factor of it). Hence, the entropy for key and nonce are 32 bits. Exhausting both of them at the same time requires $2^{64}$ trials... or really?

Because the cipher is under GCM and with a known AAD, given a key $k$ and a ciphertext $c$, we can compute $\text{GHASH}_{k,c}(\text{AAD})$.

Consider the GCM mode with its tag generation. The tag generation is given by $\text{tag} = E_k(\text{nonce}) \oplus \text{GHASH}_{k,c}(\text{AAD})$. Therefore, with known key $k$, one can find out the key-correspondent nonce by $\text{nonce} = D_k(\text{tag} \oplus \text{GHASH}_{k,c}(\text{AAD}))$.

Therefore we can exhaust the key $k$ with $2^{32} + 1$ trials, for each key $k$ find its corresponding $nonce$ and see whether it is the correct one.

We can even make it quickly by identifying the $\text{nonce}$ should end with \x00\x00\x00\x01 with this method, as it is using a 12-byte nonce.

We initially use Sage to deal with the challenge, but it was way too slow (to generate the possible keys) and decided to use Python instead. But we don't want to use other language other than Sage to generate the keys...

So what we have done is a simple multi-thread Sage key generator and a Python solver. And it was wayyyyyyyyyyyy too slow... even with pypy.

Both the key generator and the pypy solver are terribly slow. I cannot find a simple GHASH implementation to do the brute-forcing part. Computing $2^{16}$ keys takes me more than 3 mins in pypy... I just wanted to use something fast to test through the keys. BearSSL saids it can process >1000MBps according to its benchmark. Maybe I should use a language with fast compiled code.

I am a Rustacean, so why not to do it in Rust? The result is blazingly fast. It could be solved within an hour with a 64-core computer (from one of my teammates). Sage was then the bottleneck, and thus I did not bother to improve the performance of the Rust solver.

I should use Rust to generate keys to speedup the whole thing, but anyway, we solved it! :)

Wrong Ring (Cryptanalysis; 936 points)

Solved by Mystiz.

Challenge Summary

I personally see this is a cumbersome math. One of my teammates pointed out that this is similar to a ring-LWE. But anyway, knowing that is a ring-LWE does not help much.

Okay, let's get back on track. A secret polynomial, $S$, is generated to derive the key. We are given eight polynomial pairs of $(A_k, B_k)$ such that $B_k(x) \equiv A_k(x)S(x) + \varepsilon_k(x)\ (\text{mod}\ p(x))$, where $\varepsilon_k$ is an error polynomial and $p(x) = x^{256} + 1486$.

Solution

Part I: Complicating the problem a bit

Let's make the polynomial concrete! Define:

\[A_k(x) = \sum_{i=0}^{255} a_{ki} x^i, B_k(x) = \sum_{i=0}^{255} b_{ki} x^i, \varepsilon_k(x) = \sum_{i=0}^{255} e_{ki} x^i, S(x) = \sum_{i=0}^{255} s_i x^i.\]

$a_{ki}, b_{ki}, s_i$ are all integers in the set $[0, 1486]$, while $e_{ki}$ are small real numbers.

Then we have

\[\begin{aligned} \sum_{i=0}^{255} b_{ki} x^i &\equiv \left(\sum_{i=0}^{255} a_{ki} x^i\right)\left(\sum_{i=0}^{255} s_i x^i\right) + \sum_{i=0}^{255} e_i x^i \\ &\equiv \sum_{i=0}^{510}\left(\sum_{j=\text{max}(0,i-255)}^{\text{min}(255,i)} a_{kj}s_{i-j}\right)x^i + \sum_{i=0}^{255} e_i x^i \\ &\equiv \sum_{i=0}^{255}\left(\sum_{j=\text{max}(0,i-255)}^{\text{min}(255,i)} a_{kj}s_{i-j}\right)x^i + \sum_{i=256}^{510}\left(\sum_{j=\text{max}(0,i-255)}^{\text{min}(255,i)} a_{kj}s_{i-j}\right)x^i + \sum_{i=0}^{255} e_i x^i \\ &\equiv \sum_{i=0}^{255}\left(\sum_{j=0}^i a_{kj}s_{i-j}\right)x^i + \sum_{i=256}^{510}\left(\sum_{j=i-255}^{255} a_{kj}s_{i-j}\right)x^i + \sum_{i=0}^{255} e_i x^i \\ &\equiv \sum_{i=0}^{255}\left(\sum_{j=0}^i a_{kj}s_{i-j}\right)x^i - 1486\sum_{i=256}^{510}\left(\sum_{j=i-255}^{255} a_{kj}s_{i-j}\right)x^{i-256} + \sum_{i=0}^{255} e_i x^i \\ &\equiv \sum_{i=0}^{255}\left(\sum_{j=0}^i a_{kj}s_{i-j}\right)x^i - 1486\sum_{i=0}^{254}\left(\sum_{j=i+1}^{255} a_{kj}s_{i-j+256}\right)x^{i} + \sum_{i=0}^{255} e_i x^i \\ &\equiv \sum_{i=0}^{255}\left(\sum_{j=0}^i a_{kj}s_{i-j} - 1486 \sum_{j=i+1}^{255} a_{kj}s_{i-j+256} + e_i\right)x^i \\ &\equiv \sum_{i=0}^{255}\left(\sum_{j=0}^i a_{k,{i-j}}s_j - 1486 \sum_{j=i+1}^{255} a_{k,i-j+256}s_j + e_i\right)x^i \end{aligned}\]

Explanations: Under modulo $p(x)$, $x^{256} = -1486$ - so we have $$\sum_{i=256}^{510}\left(\sum_{j=i-255}^{255} a_{kj}s_{i-j}\right)x^i = - 1486\sum_{i=256}^{510}\left(\sum_{j=i-255}^{255} a_{kj}s_{i-j}\right)x^{i-256}.$$

Very complicated right? Yes... But we have a conclusion for this part:

For each $i = 0, 1, …, 255$ and $k = 1, 2, …, 8$, we have: $$b_{ki} = \sum_{j=0}^i a_{k,{i-j}}s_j - 1486 \sum_{j=i+1}^{255} a_{k,i-j+256}s_j + e_i.$$

Part II: An insight

I have noticed that the coefficients for $x^{240}, x^{241}, ..., x^{255}$ in the error polynomial would be very small (less than 0.1 in magnitude). So why don't we compare the coefficients directly?

For each $i = 240, 241, ..., 255$ and $k = 1, 2, ..., 8$, we have a corresponding equation:

\[\text{round}(b_{ki}) = \sum_{j=0}^i a_{k,{i-j}}s_j - 1486 \sum_{j=i+1}^{255} a_{k,i-j+256}s_j.\]

Since there are 256 unknowns ($s_0, s_1, ..., s_{255}$) and 256 equations, we can hopefully solve the equation. This gives us the key, hence the flag.

LOTR (Cryptanalysis; 936 points)

Solved by Mystiz.

Challenge Summary

This is an attempt to implement an anonymous signature scheme using RSA. In short, given $m$ parties with public keys being $n_1, n_2, ..., n_m$, the signature generated by this group is defined by $(c_1, c_2, ..., c_m)$, where

\[\sum_{k=1}^m \text{RSAEncrypt}(c_k, n_k)\equiv\text{hash}\ (\text{mod}\ 2^{256}),\]

and $2^{2175} + 2^{2048} \leq c_k \leq 2^{2176} - 2^{2048}$ for each of the $k$'s.

There is a catch: if $c = qn + r$ with $0 \leq r < q$, $\text{RSAEncrypt}(c, n) = qn + [r^e\ (\text{mod}\ n)]$.

Solution

Part I: Simplify the challenge as much as possible

$\text{RSAEncrypt}(qn + r, n) = qn + [r^e\ (\text{mod}\ n)]$ is cumbersome. Why don't we just assume $r = 0$ so that $\text{RSAEncrypt}$ is just an identity function?

Part II: The main dish

Note: The $c_k$ and $c_k'$ defined below are multiples of $n_k$. This is what we had from the above part for the simplicity’s sake.

My approach is to generate two ciphertexts, namely, $c_k$ and $c_k'$ for the $k$-th party. In this way, we have 243 ciphertext pairs. We are looking for $x_1, x_2, ..., x_{243}\in{0, 1}$ such that

\[\bigoplus_{k=1}^m [(1 - x_k) \text{RSAEncrypt}(c_k, n_k) + x_k \text{RSAEncrypt}(c_k', n_k)] \equiv \text{hash}\ (\text{mod}\ 2^{256}).\]

Simplifying, we have:

\[\bigoplus_{k=1}^m [x_k (c_k - c_k')] \equiv \text{hash} \oplus \bigoplus_{k=1}^m c_k\ (\text{mod}\ 2^{256}).\]

Idea: My approach is to check if one of the $2^{243}$ possible generated ciphertexts covers the target hash. If not, generate another set.

The above equation is just an linear equation! Solving it we had the values of $x_k$'s. If $x_k = 0$ we pick $c_k$, and $c_k'$ otherwise. After all we have forged a signature.

Primitive Obsession (Reverse Engineering; 936 points)

Solved by Mystiz.

Challenge Summary

This is a crackme with a 260-byte long input. Conditions involves basic math operations after casting some of the bytes into various types.

Solution

My first thought is to use Angr! Unfortunately I am not a good Angr user - so it took me a long while to give up. I have finally adopted an ultra-naive approach...

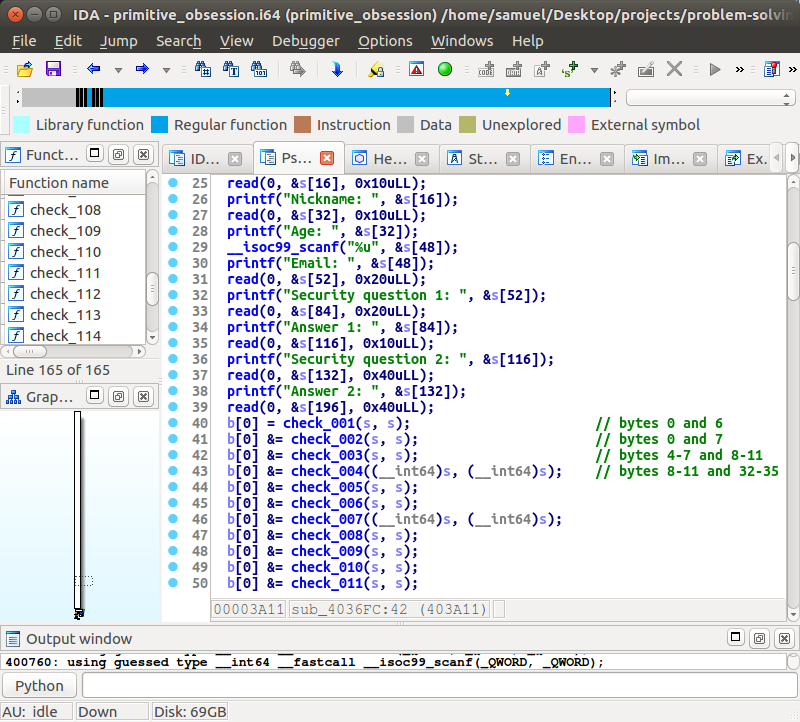
That is, I have extracted the expressions one by one manually and pass them to z3. After all, I admit my stupidity - it took me six hours to solve it...