This week, we have teamed up as @blackb6a to play CONFidence 2020 CTF. We end up ranked 15, but we are more proud of ourselves able to solve a reversing challenge called Team Trees (395 points, 5 solves).
In particular, we are the first-to-solve to the challenge. It took us around two hours to win the flag. This writeup is written by @harrier_lcc and @mystiz613.
Challenge Summary
We wanted to plant a lot of trees, but it's going kinda slow...
We are given a binary that executes a slow algorithm that takes up a lot of memory. The objective is to wait the program until it is done - the flag would be shown as the output.

Never. Our PCs don't even have enough memory to play with that. Even so, we gotta wait forever for the flag. Our objective is to optimize and rewrite the algorithm used. By optimize we mean reduce both the time and space complexities.
Solution
Part I: Baby steps from baby cases
From the binary, we knew that we are going to find $f(1337)$ for a given $f$. Although we do not know what $f$ is, we could still have an insight on it. For example, we can patch 1337 by smaller values: 0, 1, etc.:
n = 0: p4{32b9b6bca55548ed88ec405c5c7cf3a1}
n = 1: p4{ee5fadd5a727857f32b9b6bca55548ed}
n = 2: p4{ee5fadd5a727857f982d2435efffdac7}
n = 3: p4{c8b5922a9f156985b4f8094372145c13}
...
n = 4: Out of memory ;_;In particular, 32b9b6bca55548ed in the output for $n = 0$ is the v1 in sub_400816:
void __noreturn sub_400816()
{
unsigned __int64 v0; // rdx
signed __int64 v1; // rcx
signed __int64 v2; // rt0
v0 = 0x82F96AC97429A68BLL;
v1 = 0x32B9B6BCA55548EDLL;
__debugbreak();
while ( 1 )
{
v2 = v1;
v1 = 3 * v0 + 2 * v1 + 4;
v0 = v2;
}
}But what is 88ec405c5c7cf3a1? It must be related to v0 and v1. We tried 3*v0 + 2*v1 + 4 and it is ee5fadd5a727857f. It does not check out.
We have spot out that the output shares the same prefix when $n=1$ and $n=2$. Maybe we shall see what is going on with sub_400816 - it is simply generating numbers for a sequence, namely $s_n$, indefinitely:
- $s_0 = \text{82F96AC97429A68B}_{16}$,
- $s_1 = \text{32B9B6BCA55548ED}_{16}$, and
- $s_k = 3 s_{k-2} + 2 s_{k-1} + 4\mod2^{64}$ for $k \geq 2$.
Let's generate a bunch of $a_k$'s to see if there is something interesting:
s_2 = 0xee5fadd5a727857f
s_3 = 0x74ec7fe13e4ee5c9
s_4 = 0xb4f8094372145c13
s_5 = 0xc8b5922a9f156985
...If we rewrite the program output in terms of $s_k$, we have:
n = 0: p4{s_1 88ec405c5c7cf3a1}
n = 1: p4{s_2 32b9b6bca55548ed}
n = 2: p4{s_2 982d2435efffdac7}
n = 3: p4{s_5 s_4}The output when $n = 3$ is actually composed by two elements in the sequence. It makes us think: is it the case that 88ec... (also 32b9... and 982d...) is an intermediate state? To verify our thoughts, we are going to dig deeper into the assembly operations.
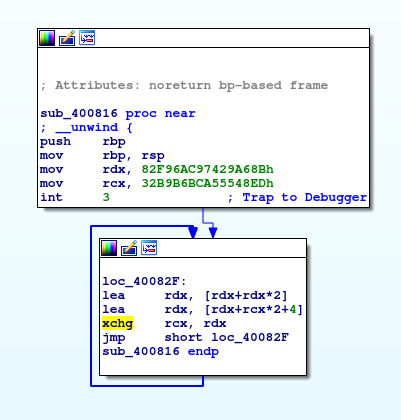
There are four operations. Here are the values of v0 and v1 (as defined in sub_400816) after each of the steps.
/* rcx = c0, rdx = d0 */
lea rdx, [rdx+rdx*2] /* rcx = c0, rdx = 3*d0 */
lea rdx, [rdx+rcx*2+4] /* rcx = c0, rdx = 3*d0 + 2*c0 + 4 */
xchg rcx, rdx /* rcx = 3*d0 + 2*c0 + 4, rdx = c0 */
jmp short loc_40082F /* rcx = 3*d0 + 2*c0 + 4, rdx = c0 */With that said, it takes four instructions for a complete cycle inside while. From the smaller values of $n$, we can see that the output format would be p4{[rdx][rcx]}. Let's see some starting values of rcx and rdx:
step | rdx | rcx
------+------------------+------------------
0 | 32b9b6bca55548ed | 82f96ac97429a68b
1 | 32b9b6bca55548ed | 88ec405c5c7cf3a1 <- output when n=0
2 | 32b9b6bca55548ed | ee5fadd5a727857f
3 | ee5fadd5a727857f | 32b9b6bca55548ed <- output when n=1
4 | ee5fadd5a727857f | 32b9b6bca55548ed ...or this?
5 | ee5fadd5a727857f | 982d2435efffdac7 <- output when n=2
6 | ee5fadd5a727857f | 74ec7fe13e4ee5c9
7 | 74ec7fe13e4ee5c9 | ee5fadd5a727857f
8 | 74ec7fe13e4ee5c9 | ee5fadd5a727857f
9 | 74ec7fe13e4ee5c9 | cb1f0980f576907d
10 | 74ec7fe13e4ee5c9 | b4f8094372145c13
11 | b4f8094372145c13 | 74ec7fe13e4ee5c9
12 | b4f8094372145c13 | 74ec7fe13e4ee5c9
13 | b4f8094372145c13 | 5ec57fa3baecb15b
14 | b4f8094372145c13 | c8b5922a9f156985
15 | c8b5922a9f156985 | b4f8094372145c13 <- output when n=3
16 | c8b5922a9f156985 | b4f8094372145c13 ...or this?
17 | c8b5922a9f156985 | 1ee81bca563d1439
18 | c8b5922a9f156985 | b053401f9467e747
19 | b053401f9467e747 | c8b5922a9f156985gdb that has a breakpoint at the beginning of the function. You are given a set of something (defined in sub_40090D) and checks if it has a given attribute (defined in sub_4009C4). If so, you call ni to move to the next step. Finally, you print the registers, extract edx and ecx, and print them as the flag.
So... what is the set of something? And what is the attribute it is checked against?
Part II: Collecting the pieces for the puzzle
There are four functions that worth investigating: sub_40090D (the enumerator), sub_4009C4 (the checker), sub_400A59 (the constructor) and sub_400840 (called from sub_40090D). We will first look into sub_400840:
_DWORD *__fastcall sub_400840(_DWORD *a1)
{
int i; // [rsp+14h] [rbp-Ch]
_DWORD *v3; // [rsp+18h] [rbp-8h]
v3 = malloc(0x20uLL);
if ( !v3 )
{
puts("Out of memory ;_;");
abort();
}
*v3 = *a1;
for ( i = 0; *a1 > i; ++i )
*(_QWORD *)&v3[2 * i + 2] = sub_400840(*(_QWORD *)&a1[2 * i + 2]);
return v3;
}Since it is allocating 32 bytes, we can define a dummy struct:
struct Dummy {
char x[32];
};Loading the struct into IDA, by redefining the types of a1 and v3 as Dummy*, we have:
Dummy *__fastcall sub_400840(Dummy *src)
{
int i; // [rsp+14h] [rbp-Ch]
Dummy *dest; // [rsp+18h] [rbp-8h]
dest = (Dummy *)malloc(0x20uLL);
if ( !dest )
{
puts("Out of memory ;_;");
abort();
}
*(_DWORD *)dest->x = *(_DWORD *)src->x;
for ( i = 0; *(_DWORD *)src->x > i; ++i )
*(_QWORD *)&dest->x[8 * i + 8] = sub_400840(*(Dummy **)&src->x[8 * i + 8]);
return dest;
}It is calling itself recursively. Would it be a deep clone? Moreover, we can further see that the first four bytes should be size and it would not be greater than 3. Otherwise 8*i+8 >= 32, overflowing the struct. After all, we think it is a node of the tree - and this is the final struct we have:
struct Node {
int size;
char x[4]; // unknown
Node *child[3];
};More importantly, we can finally claim that sub_400840 is fully reversed.
Node *__fastcall clone(Node *src)
{
int i; // [rsp+14h] [rbp-Ch]
Node *dest; // [rsp+18h] [rbp-8h]
dest = (Node *)malloc(0x20uLL);
if ( !dest )
{
puts("Out of memory ;_;");
abort();
}
dest->size = src->size;
for ( i = 0; src->size > i; ++i )
dest->child[i] = clone(src->child[i]);
return dest;
}Then we will be reversing sub_400A59. This function is simple, it is defining a path with length $n$. After the tree is constructed, it will be used by sub_400BED for enumeration. How? Let's see a baby example when $n = 2$:
digraph {
t0_0[shape=point]
t0_1[shape=point]
t0_2[shape=point]
t0_0 -> t0_1 [arrowhead=false]
t0_1 -> t0_2 [arrowhead=false]
x0[shape=point,style=invis]
y0[shape=point,style=invis]
x0->y0
t1_0[shape=point]
t1_1[shape=point]
t1_2[shape=point]
t1_3[shape=point]
t1_0 -> t1_1 [arrowhead=false]
t1_1 -> t1_2 [arrowhead=false]
t1_1 -> t1_3 [arrowhead=false]
x1[shape=point,style=invis]
y1[shape=point,style=invis]
x1->y1
t2_0[shape=point]
t2_1[shape=point]
t2_2[shape=point]
t2_3[shape=point]
t2_4[shape=point]
t2_0 -> t2_1 [arrowhead=false]
t2_1 -> t2_2 [arrowhead=false]
t2_1 -> t2_3 [arrowhead=false]
t2_1 -> t2_4 [arrowhead=false]
x2[shape=point,style=invis]
y2[shape=point,style=invis]
x2->y2
t3_0[shape=point]
t3_1[shape=point]
t3_2[shape=point]
t3_3[shape=point]
t3_4[shape=point]
t3_0 -> t3_1 [arrowhead=false]
t3_0 -> t3_3 [arrowhead=false]
t3_1 -> t3_2 [arrowhead=false]
t3_3 -> t3_4 [arrowhead=false]
x3[shape=point,style=invis]
y3[shape=point,style=invis]
x3->y3
t4_0[shape=point]
t4_1[shape=point]
t4_2[shape=point]
t4_3[shape=point]
t4_4[shape=point]
t4_5[shape=point]
t4_0 -> t4_1 [arrowhead=false]
t4_0 -> t4_3 [arrowhead=false]
t4_1 -> t4_2 [arrowhead=false]
t4_3 -> t4_4 [arrowhead=false]
t4_3 -> t4_5 [arrowhead=false]
x4[shape=point,style=invis]
y4[shape=point,style=invis]
x4->y4
u[label="...", shape=plaintext]
x5[shape=point,style=invis]
y5[shape=point,style=invis]
x5->y5
t5_0[shape=point]
t5_1[shape=point]
t5_2[shape=point]
t5_3[shape=point]
t5_4[shape=point]
t5_5[shape=point]
t5_6[shape=point]
t5_7[shape=point]
t5_8[shape=point]
t5_9[shape=point]
t5_10[shape=point]
t5_11[shape=point]
t5_12[shape=point]
t5_0 -> t5_1 [arrowhead=false]
t5_0 -> t5_2 [arrowhead=false]
t5_0 -> t5_3 [arrowhead=false]
t5_1 -> t5_4 [arrowhead=false]
t5_1 -> t5_5 [arrowhead=false]
t5_1 -> t5_6 [arrowhead=false]
t5_2 -> t5_7 [arrowhead=false]
t5_2 -> t5_8 [arrowhead=false]
t5_2 -> t5_9 [arrowhead=false]
t5_3 -> t5_10 [arrowhead=false]
t5_3 -> t5_11 [arrowhead=false]
t5_3 -> t5_12 [arrowhead=false]
{rank=same; t0_1; u; x0; y0; x1; y1; x2; y2; x3; y3; x4; y4; x5; y5}
}Well... it is just enumerating all the ternary trees with depth $n$, where each of the leaf node is on level $n$.
After that, we check the number of good trees. By good it is defined by (former) sub_4009C4:
signed __int64 __fastcall is_good_tree(Node *node, int k)
{
int ka; // [rsp+4h] [rbp-1Ch]
int kb; // [rsp+4h] [rbp-1Ch]
int i; // [rsp+1Ch] [rbp-4h]
ka = k;
if ( node->size > 1 && k )
return 0LL;
if ( node->size > k )
ka = node->size;
kb = ka - 1;
if ( kb < 0 )
kb = 0;
for ( i = 0; node->size > i; ++i )
{
if ( (unsigned __int8)is_good_tree(node->child[i], kb) != 1 )
return 0LL;
}
return 1LL;
}harrier has implemented a good tree checker (himself) in Discord for me to test with:
After all, a tree is said to be good if both of the condition are satisfied:
- for each node with two children, every children should have at most one children, and
- for each node with three children, every children and their grandchildren should have at most one children.
Cool. We have the pieces of the puzzle gathered. Define $g(n)$ to be the number of good trees of depth $n$. We are going to find $g(1337)$ and move the sequence forward by $g(1337)$ instructions.
Part III: Verifying this for the baby cases
We are double checking if our observation checks out for smaller $n$'s. From above, $g(0) = 1$, $g(1) = 3\ \text{or}\ 4$, $g(2) = 5$ and $g(3) = 15\ \text{or}\ 16$.
For $n = 0$, the only tree would be:
digraph {
node[shape=point]
edge[arrowhead=false]
t0
}Yeah. It is a good tree. Thus $g(0) = 1$. Also, $g(1) = 3$ since the three trees are all good:
digraph {
node[shape=point]
edge[arrowhead=false]
t0_0 -> t0_1
t1_0 -> t1_1
t1_0 -> t1_2
t2_0 -> t2_1
t2_0 -> t2_2
t2_0 -> t2_3
}For $n = 2$, we start rejecting trees. There are 39 trees, but there are only five being good. Hence $g(2) = 5$.
digraph {
node[shape=point]
edge[arrowhead=false]
t0_0 -> t0_1
t0_1 -> t0_2
t3_0 -> t3_1
t3_1 -> t3_2
t3_1 -> t3_3
t4_0 -> t4_1
t4_1 -> t4_2
t4_1 -> t4_3
t4_1 -> t4_4
t1_0 -> t1_1
t1_0 -> t1_2
t1_1 -> t1_3
t1_2 -> t1_4
t2_0 -> t2_1
t2_0 -> t2_2
t2_0 -> t2_3
t2_1 -> t2_4
t2_2 -> t2_5
t2_3 -> t2_6
}And $g(3) = 15$. They are:
digraph {
node[shape=point]
edge[arrowhead=false]
t0_0 -> t0_1
t0_1 -> t0_2
t0_2 -> t0_3
t5_0 -> t5_1
t5_1 -> t5_2
t5_2 -> t5_3
t5_2 -> t5_4
t6_0 -> t6_1
t6_1 -> t6_2
t6_2 -> t6_3
t6_2 -> t6_4
t6_2 -> t6_5
t3_0 -> t3_1
t3_1 -> t3_2
t3_1 -> t3_3
t3_2 -> t3_4
t3_3 -> t3_5
t4_0 -> t4_1
t4_1 -> t4_2
t4_1 -> t4_3
t4_1 -> t4_4
t4_2 -> t4_5
t4_3 -> t4_6
t4_4 -> t4_7
t1_0 -> t1_1
t1_0 -> t1_2
t1_1 -> t1_3
t1_2 -> t1_4
t1_3 -> t1_5
t1_4 -> t1_6
t7_0 -> t7_1
t7_0 -> t7_2
t7_1 -> t7_3
t7_2 -> t7_4
t7_3 -> t7_5
t7_4 -> t7_6
t7_4 -> t7_7
t8_0 -> t8_1
t8_0 -> t8_2
t8_1 -> t8_3
t8_2 -> t8_4
t8_3 -> t8_5
t8_4 -> t8_6
t8_4 -> t8_7
t8_4 -> t8_8
t9_0 -> t9_1
t9_0 -> t9_2
t9_1 -> t9_3
t9_2 -> t9_4
t9_3 -> t9_5
t9_3 -> t9_6
t9_4 -> t9_7
}digraph {
node[shape=point]
edge[arrowhead=false]
t10_0 -> t10_1
t10_0 -> t10_2
t10_1 -> t10_3
t10_2 -> t10_4
t10_3 -> t10_5
t10_3 -> t10_6
t10_4 -> t10_7
t10_4 -> t10_8
t11_0 -> t11_1
t11_0 -> t11_2
t11_1 -> t11_3
t11_2 -> t11_4
t11_3 -> t11_5
t11_3 -> t11_6
t11_4 -> t11_7
t11_4 -> t11_8
t11_4 -> t11_9
t12_0 -> t12_1
t12_0 -> t12_2
t12_1 -> t12_3
t12_2 -> t12_4
t12_3 -> t12_5
t12_3 -> t12_6
t12_3 -> t12_7
t12_4 -> t12_8
t13_0 -> t13_1
t13_0 -> t13_2
t13_1 -> t13_3
t13_2 -> t13_4
t13_3 -> t13_5
t13_3 -> t13_6
t13_3 -> t13_7
t13_4 -> t13_8
t13_4 -> t13_9
t14_0 -> t14_1
t14_0 -> t14_2
t14_1 -> t14_3
t14_2 -> t14_4
t14_3 -> t14_5
t14_3 -> t14_6
t14_3 -> t14_7
t14_4 -> t14_8
t14_4 -> t14_9
t14_4 -> t14_10
t2_0 -> t2_1
t2_0 -> t2_2
t2_0 -> t2_3
t2_1 -> t2_4
t2_2 -> t2_5
t2_3 -> t2_6
t2_4 -> t2_7
t2_5 -> t2_8
t2_6 -> t2_9
}Cool! Everything checks out! Luckily the memory overflows when $n = 4$, otherwise our OCD would be forcing us to find $g(4)$ and the writeup will be flooded by a large forest.
Part IV: Algorithms, algorithms everywhere
In this part, harrier and I work on a different topic:
- harrier's task: Find $g(1337)$.
- Mystiz's task: Find the flag if harrier has $g(1337)$ computed.
4.1. What is $g(1337)$?
To find the number of good trees of height $h$, we define an auxiliary variable $k$ (interpret it as cooldown). Here we redefine good trees again:
For a ternary tree, it is said to be good if for every node,
- [Recovery] if $k > 0$: there should be at most one child, and
- [Fertility] if $k = 0$: if there are $c$ children, then each of them has cooldown $k = c-1$.
Simply put, you need to recover to be fertile. For instance, the following is a good tree since each of the node with non-zero cooldown has only a child.
digraph {
node[shape=rectangle, style=rounded]
t0 [label=0]
t1 [label=1]
t2 [label=1]
t3 [label=0]
t4 [label=0]
t0->t1
t0->t2
t1->t3
t2->t4
}However, this is not a good tree since the red node is too fertile:
digraph {
node[shape=rectangle, style=rounded]
t0 [label=0]
t1 [label=1, style="filled, rounded", fillcolor="#ff000080"]
t2 [label=1]
t3 [label=0]
t4 [label=0]
t5 [label=0]
t0->t1
t0->t2
t1->t3
t1->t4
t2->t5
}Luckily, we don't need to count the good trees one by one. It can be solved by dynamic programming rather easily. Let's define the state dp[h][k] to be the number of good trees if the tree is of depth h and cooldown k. Then:
- [Base case]
dp[0][k] == 1for everyk, - [Transition]
dp[h][k] == dp[h-1][k-1]forh, k > 0, and - [Transition]
dp[h][0] == dp[h-1][0] + dp[h-1][1]**2 + dp[h-1][2]**3forh > 0.
The first condition is obvious - the only tree with depth 0 is the tree with the only root node. It is good no matter what the cooldown is.
For the second condition, it is not difficult to imagine it as an tree that must cooldown. Hence, if $\text{GT}_{hk}$ is a good tree with height $h>0$ and cooldown $k>0$, then:
digraph {
node[shape=point]
edge[arrowhead=false]
x->st
subgraph cluster {
style=filled
color=lightgray
label="GTₕ₋₁,ₖ₋₁"
labelloc=b
st[shape=triangle, height=2, label=""]
}
}It is a little bit tricky for the third condition. Since it is in the fertile mode again, we can decide if there are one, two or three children. Then each of the following trees work:
digraph {
node[shape=point]
edge[arrowhead=false]
x0->st0
subgraph cluster0 {
style=filled
color=lightgray
label="GTₕ₋₁,₀"
labelloc=b
st0[shape=triangle, height=2, label=""]
}
x1->st1:n
x1->st2:n
subgraph cluster1 {
style=filled
color=lightgray
label="Each subtree is GTₕ₋₁,₁"
labelloc=b
st1[shape=triangle, height=2, label=""]
st2[shape=triangle, height=2, label=""]
}
x2->st3:n
x2->st4:n
x2->st5:n
subgraph cluster2 {
style=filled
color=lightgray
label="Each subtree is GTₕ₋₁,₂"
labelloc=b
st3[shape=triangle, height=2, label=""]
st4[shape=triangle, height=2, label=""]
st5[shape=triangle, height=2, label=""]
}
}Hence, if there are k children, then there are dp[h-1][k-1]**k choices. Since we are able to pick k = 1, 2, 3, we can simply sum them up for dp[h][k]. After all, this is the Python script to compute:
def g(k: int) -> int:
# Base case
dp = [[1, 1, 1]]
# Transition
for _ in range(k):
dp.append([
sum([dp[-1][i]**(i+1) for i in range(3)]), dp[-1][0], dp[-1][1]
])
return dp[-1][0]But the numbers is growing exponentially and finding $g(1337)$ takes eternally. What can we do? Nevermind, we will get back to this shortly.
4.2. Fast sequence generation
To compute the values of ecx and edx, we can find the number of executed instructions (denote it as $q$). Since the loop is completed every four steps, we can find $s_{\mathbf{floor}(q/4)}$ and $s_{\mathbf{floor}(q/4)+1}$ and perform the remainder of the instructions.
Let's get back to the sequence $s_n$:
- $s_0 = \text{82F96AC97429A68B}_{16}$,
- $s_1 = \text{32B9B6BCA55548ED}_{16}$, and
- $s_k = 3 s_{k-2} + 2 s_{k-1} + 4\mod2^{64}$ for $k \geq 2$.
To compute it efficiently, we can rewrite it as a matrix notation:
\[ \begin{bmatrix} s_{k+1} \\ s_k \\ 1 \end{bmatrix} = \begin{bmatrix} 2 & 3 & 4 \\ 1 & 0 & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix} s_k \\ s_{k-1} \\ 1 \end{bmatrix} \mod 2^{64}. \]
Why? Try the multiplication by yourselves! Anyway, then we are able to compute $s_m$ and $s_{m+1}$ efficiently, since
\[ \begin{bmatrix} s_{m+1} \\ s_m \\ 1 \end{bmatrix} = \begin{bmatrix} 2 & 3 & 4 \\ 1 & 0 & 0 \\ 0 & 0 & 1\end{bmatrix}^m \begin{bmatrix} s_1 \\ s_0 \\ 1 \end{bmatrix} \mod 2^{64}. \]
Moreover, since
\[\begin{bmatrix} 2 & 3 & 4 \\ 1 & 0 & 0 \\ 0 & 0 & 1\end{bmatrix}^{2^{64}} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}, \]
the square matrix has order $2^{64}$. That said, we don't need to find the exact value for $g(1337)$. Instead, we can compute $g(1337)\mod (2^{64}\times4)$. Hereby we need to multiple the number by four, since there are 4 instructions per loop).
Part V: The flagggggggggg!
After all, we can modify the Python function we had to compute $g(k)\mod 2^{66}$:
def g(k: int) -> int:
# Base case
dp = [[1, 1, 1]]
# Transition
for _ in range(k):
dp.append([
sum([dp[-1][i]**(i+1) for i in range(3)]) % 2**66, dp[-1][0], dp[-1][1]
])
return dp[-1][0]And g(1337) = 59988074356265869957 pops out at no time. Therefore, we can find $s_{14997018589066467489}$ and $s_{14997018589066467490}$ and proceed one instruction further. We have rdx being 0x62246322232ceabf and rcx being 0xbf1d9826c054007!
Thus p4{62246322232ceabfbf1d9826c054007} would be the flag, right? NO!
It was 4:40 am and we were very sleepy. It took us few minutes to figure out that rcx isn't composed of 16 hexchars. The correct flag should be p4{62246322232ceabf0bf1d9826c054007} (note that there is an zero). Yeah, :checkered_flag: - and we are the first to capture this!