Welcome!! (23 points, 663 solves)

Difficulty: Warm-up

We surely did get warmed up this CTF, as we came second, even beating the Cryptohackers (merge) team! Well done to everyone who participated đź’ś

Did it! (33 points, 220 solves)

Difficulty: Easy

The parameters $n = 127$ and $\ell = 20$ is fixed. A hidden subset of $\ell$ numbers $S \subseteq \{0, 1, \cdots, n - 1\}$ with $|S| \leq \ell$ is chosen, and we are given $13$ calls to the following oracle: Given a set $T \subseteq {0, 1, \cdots, n - 1}$ also with $|T| \leq \ell$, the server computes $T \setminus S$ and outputs $\{(u^2 + \varepsilon) \pmod{n} : u \in T \setminus S, \varepsilon \in \{0, 1\}\}$.

Solution 1 (TWY): Note that there are only $\frac{n - 1}{2}$ quadratic residues modulo $n$ and their distribution is pseudorandom. Hence, we can partition them into several sets such that in each set, the quadratic residues are all “spaced out” i.e. differ by $2$ or more. Then, we can uniquely decode the output from the oracle, allowing us to recover $S$.

Solution 2 (grhkm): We simply throw random oracle calls $T$ at the server and see whether any of the elements from $T$ cannot possibly by in $T \setminus S$, i.e. neither $u^2 \pmod{n}$ nor $(u^2 + 1) \pmod{n}$ is in the server output. Then, those must be in $S$. Repeat this until we recover $S$.

Blue Office (36 points, 181 solves)

Difficulty: Easy

We are given a simple stream cipher with a custom seed generation function and a LCG reseeding function. Literally every part of the cipher is weak, but we can focus on lines 9 and 10:

def reseed(s):
    return s * 214013 + 2531011

def encrypt(s, msg):
    assert s <= 2**32
    c, d = 0, s
    enc, l = b'', len(msg)
    while c < l:
        d = reseed(d)
        enc += (msg[c] ^ ((d >> 16) & 0xff)).to_bytes(1, 'big') 
        c += 1
    return enc

The message is xor’ed with (d >> 16) & 0xff, which is bit 16 to 23 of d. Since reseed is a LCG, we can just bruteforce all seeds s <= 2**24 and compute d also mod 2**24.

Suction (41 points, 151 solves)

Difficulty: Easy

RSA parameters with $p, q \sim 2^{128}$ and $e \sim 2^{16}$ are generated. However, we are only given $N' = \lfloor pq / 2^8 \rfloor$ and $e' = \lfloor e / 2^8 \rfloor$. This is not a problem to us, as we know that $N \in [2^8 pq, 2^8 pq + 2^8)$. We used our teammate TWY’s computer to factor all these numbers. To quote, “it took 4 seconds”. (4 seconds is the time to test $e$ lul)

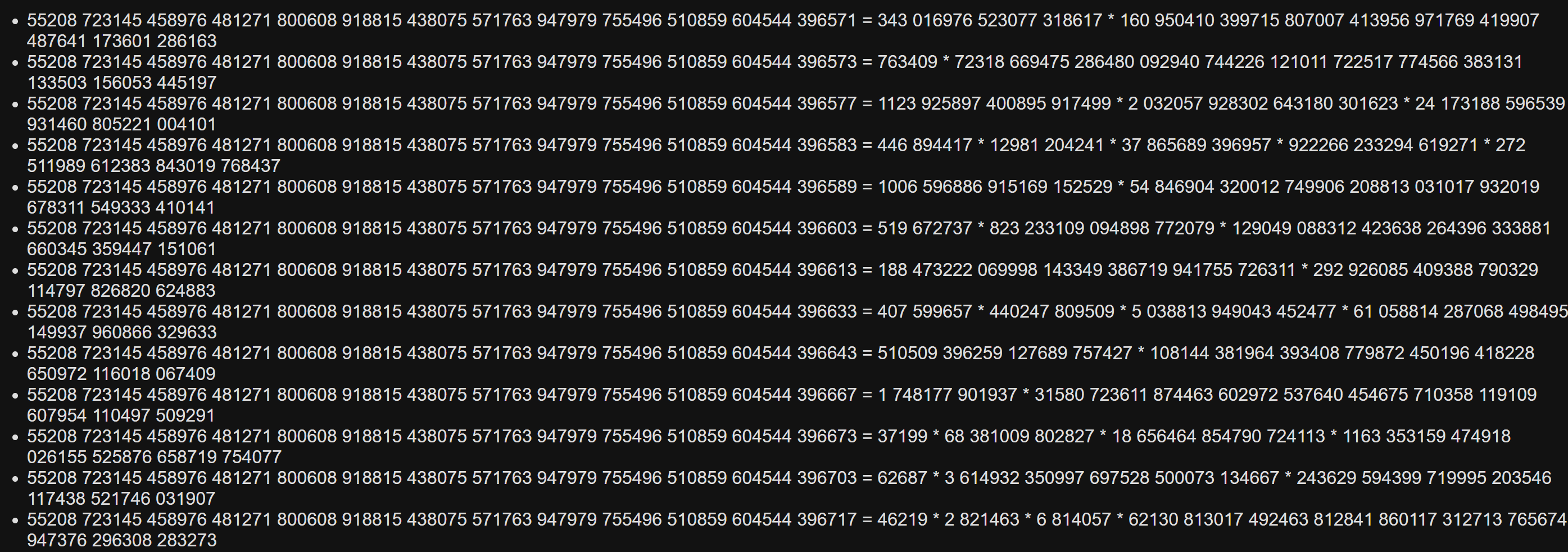(All primes and numbers with any factor less than 10000 have been eliminated before factoring.)

In the end, we see that $N = N' + 69$ and $(p, q) = (188473222069998143349386719941755726311, \cdots)$, and testing the $256$ candidates for $e$ yields the flag.

Insights (59 points, 88 solves)

We are given RSA parameters with several vulnerability, the most critical one being in how the secret generation:

def genKey(L, nbit):
    p, q = [genPrime(L, nbit) for _ in '__']
    n = p * q
    d = next_prime(pow(n, 0.2919))
    phi = (p - 1) * (q - 1)
    e = inverse(d, phi)
    pubkey, privkey = (n, e), (p, q)
    return pubkey, privkey

Since we know $n$ from the output, we can just compute $d$ and decrypt the message as $m = c^d \pmod{n}$…

Resuction (64 points, 78 solves)

Similar to the setup of Suction, we are given the masked values $N'$ and $e'$ with the lower $8$ bits masked away. This time, we have another vulnerability:

def keygen(nbit, r):
    while True:
        p, q = [getPrime(nbit) for _ in '__']
        d, n = getPrime(64), p * q
        phi = (p - 1) * (q - 1)
        if GCD(d, phi) == 1:
            e = inverse(d, phi)
            N = bin(n)[2:-r]
            E = bin(e)[2:-r]
            PKEY = N + E
            pkey = (n, e)
            return PKEY, pkey

Note that $d < 2^{64}$ while $n \sim 2^{2048}$, so we can use the Wiener attack to recover $d$.

Derik (68 points, 73 solves)

We are given constants $C_0, \cdots, C_7$ and the following system of equations:

$$\begin{cases} C_0 p - C_1 q &\geq 0 \\ C_2 q - C_3 r &\geq 0 \\ C_4 r - C_5 s &\geq 0 \\ C_6 e - C_7 d &= 31337 \\ (C_0 p - C_1 q)^e + (C_2 q - C_3 r)^e + (C_4 r - C_5 s)^e &= d(C_0 p - C_1 q)(C_2 q - C_3 r)(C_4 r - C_5 s) \\ p, q, r, s, d \quad \text{are primes} \end{cases}$$

From the fourth equation, we can recover possible values of $(e, d) = (3, 73)$. This turns the fifth equation into one of the form $X^3 + Y^3 + Z^3 = 73XYZ$, which is birational equivalent to an elliptic curve. Therefore, we can recover a rational point as follows:

R = PolynomialRing(QQ, "x, y, z")
x, y, z = R.gens()
C = x**3 + y**3 + z**3 - 73 * x * y * z

phi = EllipticCurve_from_cubic(C)
E = phi.codomain()
X, Y, _ = phi.inverse()(E.gen(0))
Z = lcm(X.denom(), Y.denom())
X, Y = X * Z, Y * Z
print(X, Y, Z)
# 2848691279889518 1391526622949983 89200900157319

From here, we can make an educated guess that $(C_0p - C_1q, C_2q - C_3r, C_4r - C_5s) = \sigma(X, Y, Z)$, where $\sigma$ denotes a permutation. From this, we solve for $p, q, r$ and hence the RSA system.

There are many unintended solutions, e.g. searching for integer solutions from this paper, or from guessing parameters from parts of code that we did not cover.

ASIv1 (80 points, 59 solves)

Difficulty: Medium

The flag is encoded as a base $3$ vector $f$ in $\mathbb{F}_3^l$ with $\ell = 110$. Then, $\ell^2$ random vectors $s_i \in \mathbb{F}_3^{\ell}$ are generated, and we are given $(s_i, f \cdot s_i)$, the dot product of the vectors.

Since dot product is linear in each of the vector components, we can write out a system of $\ell^2$ linear equations in $\ell$ variables and solve for $f$.

It seems that the original solution involves adding error (and probably Arora-Ge), but I guess the challenge author messed up.

TPSD (82 points, 57 solves)

We are given many challenges $(a, b)$, and have to provide a triplet of numbers $(p, q, r)$ such that $p^3 + q^3 + r^3 = 1$, $2^{a - 1} \leq \min(|p|, |q|, |r|) \leq 2^b - 1$ and at least one of them being prime.

Solution: A set of solutions are parametrised by $(p, q, r) = (9k^4, 3k - 9k^4, 1 - 9k^3)$, so we simply increment $k$ in the range given until we encounter a solution satisfying the conditions.

Roldy (85 points, 55 solves)

The challenge is based on Order-Preserving Encryption (OPE). In short, it is a scheme such that $x < y \iff \mathrm{Enc}(x) < \mathrm{Enc}(y)$. We are given an encrypted flag and an oracle to compute the encryption of a message.

Solution: Binary search.

Blobfish (90 points, 51 solves)

We are given a password-protected compressed file (flag.zip) produced by linux zip utility, containing an image file (flag.png) with the AES-encrypted flag in hexadecimal form.

The known information is that the AES key used for encryption is a random 8-byte string repeated twice. The IV used is the MD5 digest of the key, and the zip password is the first 10 bytes of the key.

Since these parameters are all related, we can recover all of them if we can recover the password of the compressed file. We can use an existing known plaintext attack tool, bkcrack to do so.

To carry out the attack, we need some known plaintext.

PNG Format Dissection by corkami:

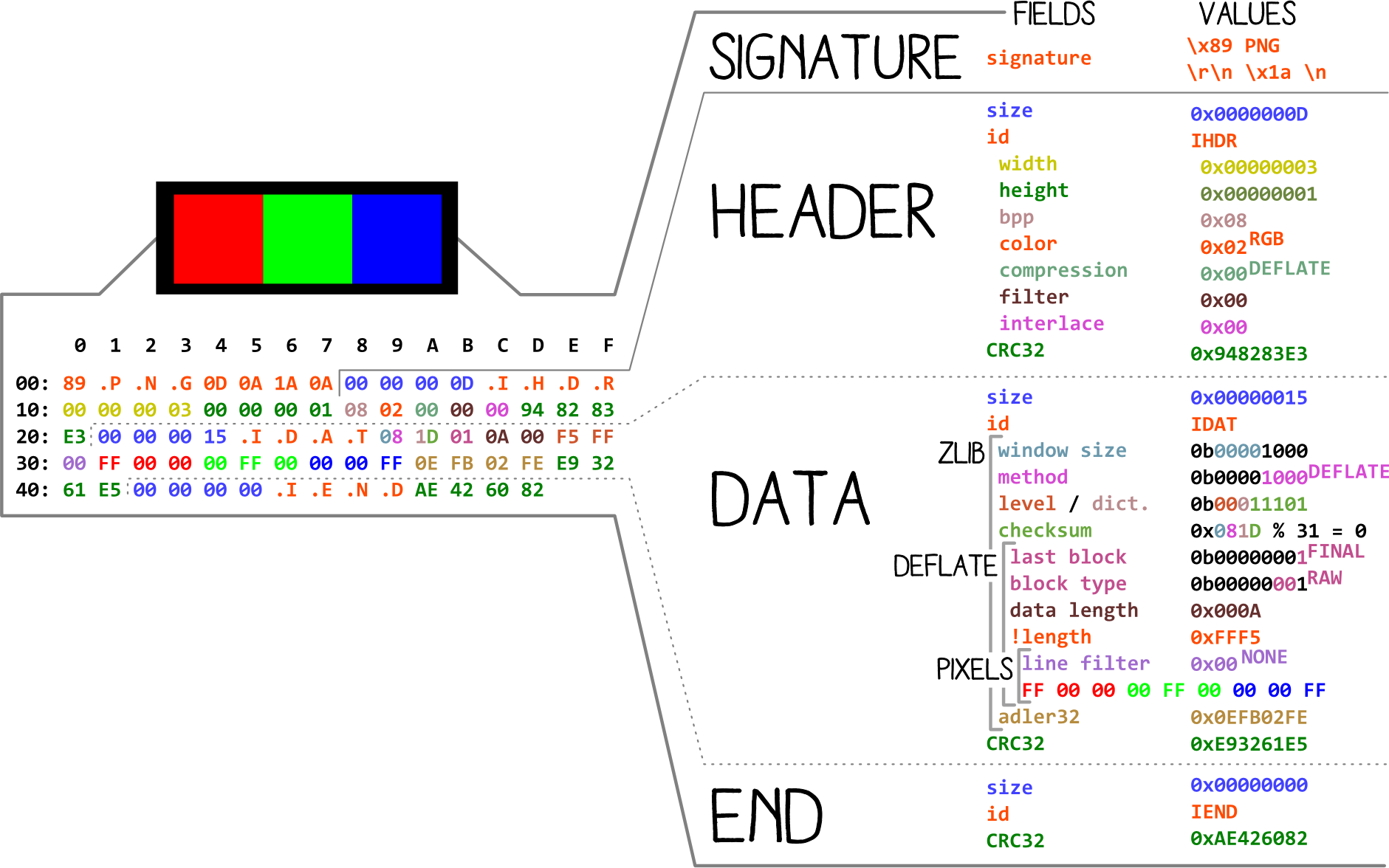
Given the fixed dimension (800x50) of flag.png, all bytes before the CRC32 checksum in the header should be fixed. Therefore we can prepare our known plaintext file as the following:

plain.txt

According to bkcrack tutorial, we can obtain the internal key using the below command:

bkcrack -C flag.zip -c flag.png -p plain.txt

After a while the key 03492be6 b81a5123 24d7b146 will appear.

We can then recover the original password using another command:

bkcrack -k 03492be6 b81a5123 24d7b146 -r 10 ?b

After several seconds, a password ad 6e fb 79 2a ea 5a aa ad 6e (as bytes) should show up.

We can extract flag.png using this binary password. After that, we can use bytes.fromhex("ad 6e fb 79 2a ea 5a aa") * 2 as the AES key and the MD5 hash of the key as IV to recover the flag.

Trex (100 points, 45 solves)

We are given twenty random challenges $a \leq 2^{132}$, and we have to provide three distinct nonzero integers $x, y, z$ such that $x^2 - xy + y^2 = az^3$.

Solution: $(x, y, z) = (24a^2, -24a^2, 12a)$ (More generally, a possible generating formula is $(x, y, z) = (3k^3 a^2, -3k^3 a^2, 3k^2 a)$).

Note from grhkm: I spent an embarrassingly long time trying to factor $4a^4$ over $\mathbb{Q}[\sqrt{-3}]$, since any solution on $(x + y)^2 + 3(x - y)^2 = 4az^3$ where $(x + y, x - y) \in \mathbb{Q}$ yields a solution. Thank you to TWY for pointing out the solution above…

Risk (122 points, 35 solves)

We are given a RSA scheme $(n, e) = (pq, rs)$ where $(p, r), (q, s) \leftarrow \textrm{getPrime}(m, 2048)$ and $m$ being a hidden integer. Let us inspect getPrime:

def genPrime(m, nbit):
    assert m >= 2
    while True:
        a = getRandomNBitInteger(nbit // m)
        r = getRandomNBitInteger(m ** 2 - m + 2)
        p = a ** m + r
        if isPrime(p):
            return (p, r)

Since we have $e = rs$, which is $28$ bits, we can deduce that $m = 4$, and also that $(r, s) = (10728, 14071)$. This means that $n = pq = (a^4 + 10728)(b^4 + 14071)$, where $a, b \sim 2^{256}$. From this, it is clear that $n \approx a^4b^4$, and indeed we have $ab = \lfloor n^{1 / 4} \rfloor$. Therefore, we can write $b = \lfloor n^{1 / 4} \rfloor / a$, substitute into $n = (a^4 + 10728)(b^4 + 14071)$, and recover the factorisation.

Keymoted (146 points, 28 solves)

We are given a complicated scheme, so we will not describe the scheme itself, but rather highlight the key points and how to solve it. Firstly, a RSA modulus $n$ is generated as follows:

nbit = 256
p = getPrime(nbit)
_s = p ^^ ((2 ** (nbit - 1)) + 2 ** (nbit // 2))
q = next_prime(2 * _s + 1)
n = p * q

Line 2 shows that $s' = p - 2^{b - 1} \pm 2^{\lfloor b / 2 \rfloor}$, meaning that $q \sim 2(p - 2^{\lfloor b / 2 \rfloor})$. Therefore, $n \sim 2p(p - 2^{\lfloor b / 2 \rfloor})$. Therefore, we can solve for an approximation to $p$, then test $p \in [\tilde{p} - \epsilon, \tilde{p} + \epsilon]$.

From here, we are presented with the encryption scheme itself. First, random parameters $a, b$ are generated. Then, to encrypt a message $m$, we first increment $m$ until $m^3 + am + b$ is a quadratic residue both modulo $p$ and modulo $q$. Next, we compute $y = \sqrt{m^3 + am + b} \pmod{n}$ by CRT. Finally, the encryption is the point $[65537](m, y)$, where $[\cdot]$ denotes scalar multiplication and $(m, y) \in E / \mathbb{Z}_n : y^2 = x^3 + ax + b$.

To decrypt this encryption, we simply note that $E / \mathbb{Z}_n \cong E / \mathbb{F}_p \times E / \mathbb{F}_q$, so we can decrypt on the elliptic curves modulo $p$ and $q$ respectively, then combine the plaintexts with CRT. Decrypting the message modulo a prime is simple, as we simply compute $[65537^{-1}]P$, where $65537^{-1}$ is computed modulo the order of the curve.

Barak (150 points, 27 solves)

We are given an algebraic object Barak along with operations like on_barak, add_barak and mul_barak. We then have to solve a discrete logarithm problem:

FLAG = flag.lstrip(b'CCTF{').rstrip(b'}')
P = rand_barak(E)
m = bytes_to_long(FLAG) 
assert m < p
Q = mul_barak(m, P, E)

Let us first inspect the code of on_barak:

def on_barak(P, E):
    c, d, p = E
    x, y = P
    return (x**3 + y**3 + c - d*x*y) % p == 0

...

p = 73997272456239171124655017039956026551127725934222347
d = 68212800478915688445169020404812347140341674954375635
c = 1
E = (c, d, p)

From this, we see that the algebraic objects given are indeed points on the curve $E / \mathbb{F}_p: x^3 + y^3 - dxy + 1 = 0 \pmod{p}$. Since it contains a rational point, say $(x, y) = (-1, 0)$, we know that it is birational to an elliptic curve. Using Sage, we can compute the equivalent model:

p = 73997272456239171124655017039956026551127725934222347
d = 68212800478915688445169020404812347140341674954375635
c = 1

R.<x, y, z> = GF(p)[]
C = x^3 + y^3 - d * x * y * z + c * z^3
E = EllipticCurve_from_cubic(C)
print(E) # Elliptic Curve defined by y^2 = x^3 + ...*x + ... over Finite Field of size ...

Note that we are usually able to compute the explicit morphism map between $C$ and $E$, but here $p$ is too large. Anyways, let us check out the parameters of $E$:

E.order().factor()
# 2^5 * 3^3 * 17 * 2341 * 23497 * 500369 * 5867327 * 33510311 * 13824276503 * 67342255597

We see that $|E / \mathbb{F}_p|$ is relatively smooth, meaning that we can perform a Pohlig-Hellman attack on the problem.

Big (169 points, 23 solves)

We are presented with a known-plaintext setup on a custom scheme. Firstly, the key generation is as follows:

def genkey(nbit):
    while True:
        p = getPrime(nbit)
        if p % 4 == 3:
            q = int(str(p)[::-1])
            if isPrime(q):
                return p * q, (p, q)

This means that $n = pq = p \cdot \mathrm{rev}(p)$ where $\mathrm{rev}$ reverses the (base-$10$) digits. Hence, we can perform a digit-by-digit search on $p$ and $q$, hence recovering the factorisation of $n$.

Onto the actual scheme, let us write $\left(\cdot / \cdot\right)$ for the Kronecker symbol, a direct generalisation of Legendre’s symbol. For each bit of the flag $f_i$, we are given integers $s_i$ where $s_i = t_i - at_i^{-1} \pmod{n}$, $a$ is a given constant such that $\left(a / n\right) = 1$, and $\left(t_i / n\right) = 2f_i - 1 \in \{-1, 1\}$.

To recover $f_i$, we can first solve for $t_i$ by solving the quadratic equation $t_i^2 - s_it_i + a \equiv 0 \pmod{n}$, where the factorisation of $n$ is known from above. Then, we simply evaluate $\left(t_i / n\right)$ to get the flag bits.

Byeween (174 points, 22 solves)

We are given an elliptic curve over the rationals $E / \mathbb{Q}$ and a point $Q \in E / \mathbb{Q}$, and we have to provide all the points $P$ such that $2P = Q$.

Overcomplicated solution by grhkm: It is believed that $E / \mathbb{Q}$ has rank $0$ or $1$ for asymptotically $100%$ of the time, with the average rank of elliptic curves being $\frac{1}{2}$. Since we are given a rational point on the curve, it will almost always have rank $1$. Therefore, $Q$ can be written as a multiple of the unique generator $G$ of the group, and we can compute a solution to $2P = Q$. From here, all remaining solutions are given by $P' = P + R$, where $R \in E[2]$ i.e. $2R = O$. These are given by $R = (x, 0)$ for the model $y^2 = f(x)$.

Bertrand (180 points, 21 solves)

Difficulty: Medium

We are given a 256x256 grayscale png. The flag is padded with printable chars to have length $256^2$ and then encypted with an unknown key in $\mathbb{Z}_{256}^3$ as the pixels of the png.

If the relative order of the 3 elements in the unknown key $(k_1, k_2, k_3)$ is fixed, the pixels are in the form of $x_i = flag_{p_i} + c_{i,1} k_1 + c_{i,2} k_2 + c_{i,3} k_3 \text{ mod } 256$ where $p$ is a permutation. For each of the relative orders of $k_1$, $k_2$ and $k_3$, $p_i$ and $c_{i,j}$ can be found by slightly modifying the encyption script.

Notice that $(c_{i,1}, c_{i,2}, c_{i,3})$ often equals to one of $(3, 0, 0)$, $(0, 3, 0)$, $(0, 0, 3)$. As $x_i$ is known and $flag_{p_i}$ has a capped range (printable chars), they can be used to eliminate most of the possibities of $k_j$.

Only a few possibilites of $(k_1, k_2, k_3)$ left after that, exhausting them will give the flag.

Shefid (209 points, 17 solves)

Difficulty: Hard

We are presented with exactly the SIDH scheme.

Solution: Perform Castryck and Decru’s attack on SIDH.

Slowsum (209 points, 17 solves)

Difficulty: Tough (?)

We are given the following interesting scheme (NB: Slightly modified):

  1. Hash
    • The hash function $H(f)$, where $f \in \mathbb{F}_q[x]$, is defined as $$H(f) = f(1)^{\left(\frac{q - 1}{2} - f(1)\right)} \pmod{q}$$
  2. Setup
    • Define $q = 113$
    • We send parameters $n \geq 5$ and $d \geq 3$ such that $nd \geq q$
    • Define $R = \mathbb{F}_q[x_1, \cdots, x_n]$
    • We send a polynomial $f_0(x_1, \cdots, x_n) \in R$ with $\deg(f_0) = d$.
    • A checksum $h_0 = \sum_{\mathbf{x} \in \{0, 1\}^n} f(\mathbf{x})$ is computed
  3. Verification
    • We send a sequence of data $(f_1, h_1), \cdots, (f_n, h_n)$ such that
      • Polynomial: $f_i \in \mathbb{F}_q[x]$ is a univariate polynomial.
      • Degree: $\deg(f_i) \leq d$
      • Check 1: For $i \geq 2$, $f_i(0) + f_i(1) = f_{i - 1}(h_{i - 1})$
      • Check 2: $H(f_i) = h_i$
    • Final check: $f_0(h_1, \cdots, h_n) = f_n(h_n)$
    • If all checks pass and $f_1(0) + f_1(1) = h_0$, the flag is given.

If you are looking at this and wondering what is going on, no worries, so am I. Nevertheless, the solution is pretty simple. We note that $H(f)$ is quite weak. For example, $H(x^k) = 1$ for any $k$. Therefore, the following parameters work:

$$\begin{aligned} & n = 5, d = 25 \\ & f_0 = x_1^{25} \implies h_0 = 16 \\ & (f_i, h_i) = (x^i, 1) \end{aligned}$$

This works as for the final check, $f_0(1, \cdots, 1) = 1$ and of course $f_n(h_n) = 1$.

Vinefruit (194 point, 19 solves)

We are presented with a rolling hash $H_i(m) = c_i + \sum_j m_j p_i^j \pmod{2^{b_i}}$, where $(c_i, p_i, b_i)$ are one of three parameter sets (2166136261, 16777619, $2^{16}$), (14695981039346656037, 1099511628211, $2^{32}$), (144066263297769815596495629667062367629, 309485009821345068724781371, $2^{64}$). We are then asked to provide message collision pairs $m_1, m_2$ such that $|m_1| = |m_2| = 16$ (or longer, but we can simply add padding).

To solve this, we aim to find a vector message (with coefficients in $[32, 126]$), say $v$, such that $H_i(v) = c_i$. If we have such a message, then $H_i(m + v) = c_i + \sum_j (m_j + v_j) p_i^j = \left(c_i + \sum_j m_j p_i^j\right) + \left(H_i(v) - c_i\right) = H_i(m)$. To find such a vector, we expand the definition to get

$$ H(v) = v_1p + v_2p^2 + \cdots + v_{16}p^{16} \pmod{2^b} $$

We can solve this by LLL, since the lattice

$$\begin{aligned} M = \left(\begin{array}{c|c|c} \begin{matrix} p \\ p^2 \\ \vdots \\ p^{16} \end{matrix} & I_{16} & O \\ \hline -c_i & O & 1 \\ \hline 2^b & O & O \end{array}\right) \end{aligned}$$

spans the vector $v = \{0, v_1, v_2, \cdots, v_{16}, 1\}$. We can answer the challenges from here.